QUADRAPHONIC MATRIX MATH

This page explains the mathematics behind the quadraphonic matrix systems. The mathematic principles used are based on algebra, complex numbers, and trigonometry.

General mathematical and engineering principles used in matrix quadraphonic systems:

Mathematical principle 1: Use of logarithms and exponentials to calculate decibels (dB)
Calculating decibels:

The formulas in this section are in Microsoft Excel ^® form.
- Calculating decibels for voltage ratios:
  Value_dB = 20 * log10(voltage_ratio)
  
  Procedure: Find the common logarithm of voltage_ratio. Then multiply by 20.
- Calculating decibels for power ratios:
  Value_dB = 10 * log10(power_ratio)
  
  Procedure: Find the common logarithm of power_ratio. Then multiply by 10.
- Finding voltage ratios from decibels:
  voltage_ratio = 10 ^ (Value_dB /20)
  
  Procedure: Divide Value_dB by 20. Then raise 10 to the power of the result.
- Finding power ratios from decibels:
  power_ratio = 10 ^ (Value_dB /10)
  
  Procedure: Divide Value_dB by 10. Then raise 10 to the power of the result.
Mathematical principle 2: Solutions of systems of simultaneous equations
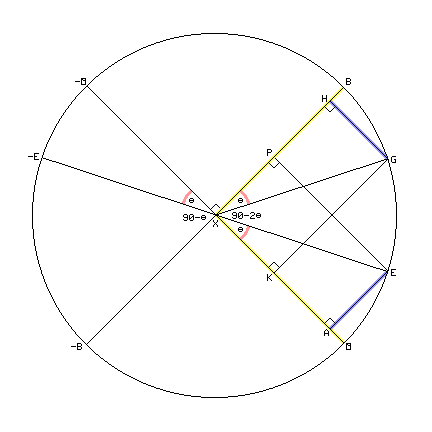
- For a solution of simultaneous equations in n variables to be unique, n equations are required.
  In quadraphonics, this would be 4 equations in 4 unknowns - a discrete quadraphonic system.
- When a system of simultaneous equations in n variables has fewer than n equations, the system normally has multiple solutions.
  Such a system can have no solution. But such systems are not used in quadraphonics.
- Encoding matrix quadraphonics uses a system of 2 equations with n variables (representing n input channels). There are 2 channels on the recording.
  In quadraphonics, this would be 2 equations in 4 unknowns.
- Decoding matrix quadraphonics uses a system of n equations with 2 variables (representing n output channels).
  In quadraphonics, this would be 4 equations in 2 unknowns.
- The system of n equations in 2 variables is used to recover the n channels. But because these systems of equations do not have a unique solution, there is crosstalk between the channels.
  But the coefficients of the two systems of equations are chosen by design to place the crosstalk where the designer wants it to be.
Engineering definition 1: The stereophonic record groove
Modulations on the stereo record groove are defined by the RIAA (Recording Industry Association of America).

Here are the stereophonic groove modulations as defined by the RIAA:
1. The stereophonic groove shall contain two channels of information recorded as orthogonal modulations of a single groove.
2. The 45 degree-45 degree system is the standard. In this system the two mutually perpendicular axes of modulation shall be symmetrically disposed with respect to a normal to the disc surface.
3. The right hand information channel, as viewed by the listener, shall appear as modulation of the outside wall of the groove.
4. When equal in-phase signals are recorded in the two channels they shall result in lateral modulation of the stereophonic groove shall produce equal in-phase acoustical signals.
5. The stereophonic groove contour shall be as recommended in RIAA Dimensional Standards for Disc Phonograph Records, Bulletin E 4.
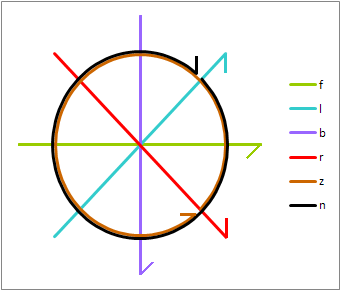
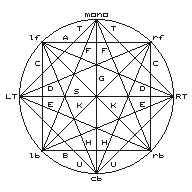
Stereo Groove Modulations

These modulations are as viewed from beyond the cartridge end of a normally mounted pickup arm:
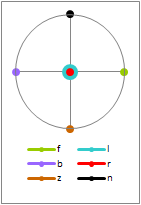
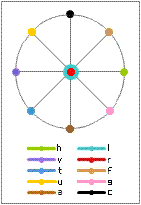
- Left and right channels:
  The left channel is recorded on the side of the groove closest to the spindle.
  - Left channel modulations slope up to the right and down to the left at a 45° angle (cyan).
  
  The right channel is recorded on the side of the groove closest to the rim.
  - Right channel modulations slope up to the left and down to the right at a 45° angle (red).
- In-phase (center) channel and reversed-phase recording:
  In-phase modulations are lateral (horizontal - olive). They emulate a monaural record.
  
  Reversed phase modulations are vertical (violet).
- Circular modulations:
  Clockwise motion (viewing the cartridge end of the tonearm) occurs when the left channel leads the right channel by 90° (black).
  
  Anticlockwise motion (viewing the cartridge end of the tonearm) occurs when the left channel lags the right channel by 90° (brown).

Basic mathematic principles of matrix quadraphonic systems:

Postulate 1: A matrix quadraphonic recording must play on and be compatible with stereo players.
Collaro size feeler

- Special equipment (including a special pickup cartridge) must not be needed to play the recording in stereo.

- Very few people will buy a recording not compatible with normal stereo equipment.

Only quadraphonic enthusiasts would be able to use it. So it is essential to make recordings fully playable on stereo players.

These rules ensure compatibility:
- Corollary 1 to Postulate 1: Quadraphonic recordings must have left-right symmetry in stereo play.
  - This is necessary to keep from overloading one side of the stereo recording.
- Corollary 2 to Postulate 1: Many parts should locate similarly in stereo and quadraphonic play.
  - The encoding and decoding methods should accomplish this.
  - Front center parts belong in the front center of both renderings.
  - Parts on the left belong on the left of both renderings.
  - Parts on the right belong on the right of both renderings.
- Corollary 3 to Postulate 1: Low bass parts must be recorded in phase in both stereo channels.
  - This is so the two stereo speakers will aid each other in reproducing the bass.
  
  - At least two of the quadraphonic speakers should be in phase to aid each other in reproducing the bass.
  
  - In addition, if the recording is on a phonograph record, the bass must be recorded laterally (in phase) in the groove.
  
  Bass recorded in other orientations must be recorded at much lower levels to avoid overcutting the groove.
- Corollary 4 to Postulate 1: Most matrix encoding systems encode center back sounds so they disappear in mono play.
  - This is a problem with most encoding systems.
  
  - Usually the recording engineer is advised to not pan important material to center back.
  
  Center back is a good place to hide some extra reverb.
- Corollary 5 to Postulate 1: Avoid Large phase differences between the left front, center front, and right front channels.
  - Large phase differences make a weird "phasiness" sensation when playing the recording in stereo.
  
  - This effect makes image location of musical parts difficult.
  
  - This unwanted effect happens with the UMX (BMX), Matrix H, Matrix E, Matrix G, and Phase Location.
  
  - Note that while the matrix decoder removes phase anomalies when decoding the record, the stereo player does not.
  
  - It is not advisable to use a matrix encoding system that shifts the phase of the front channels.
- Corollary 6 to Postulate 1: Standard radio station methods must work properly with quadraphonic recordings.
  - A radio-frequency carrier in the groove causes a swooping sound when a phonograph record is static-cued or slip-cued.
  
  Radio-frequency carriers should not be used.

Postulate 2: Linear algebra with complex numbers is sufficient to represent any quadraphonic matrix system.

Nothing in the encoding and decoding system may change the basic waveforms that are encoded. This means that the following mathematical operations must not be used on the signals:

Powers and roots
Exponentials and logarithms
Trigonometric functions*
Other Transcendental functions
Calculus

* Except where the trigonometric value is a constant used in a polynomial expression to define an encoding angle.

Corollary 1 to Postulate 2: The mathematical matrix can be used to calculate any quadraphonic matrix.

The process used for quadraphonic matrix is called matrix multiplication.

The following are the matrices used for one encode and one decode operation in matrix quadraphonics:

F ... Original 4 Channels to Encode (column vector LF, RF, LB, RB or L, R, F, B)
E ... Encoder Matrix
C ... Encoded Program for Record or Tape (column vector L, R)
D ... Decoder Matrix
S ... Decoded Output to Speakers (column vector LF, RF, LB, RB or L, R, F, B)
C = E F ... Encoding Equation
S = D C ... Decoding Equation
S = D E ... Combined Encode-Decode Effects Matrix
S = D (E F) ... Entire Encode-Decode Process

Here is an example of this use of the matrix. The Electro-Voice Stereo-4 System is shown. But it works for any matrix system.

ENCODER

DECODER

							⌈ \| \| ⌊	LF	⌉ \| \| ⌋	input matrix
								RF
								LB
C = E F								RB
						×				product
⌈ ⌊	1.0	0.3	1.0	−0.5	⌉ ⌋		⌈ ⌊	LF + 0.3 RF + LB − 0.5 RB			⌉ ⌋
	0.3	1.0	-0.5	1.0				0.3 LF + RF − 0.5 LB + RB
encoder matrix										encoded output

					⌈ ⌊	L	⌉ ⌋	encoded input
S = D C						R
				×				product
⌈ \| \| ⌊	1.0	0.2	⌉ \| \| ⌋		⌈ \| \| ⌊	L + 0.2 R			⌉ \| \| ⌋
	0.2	1.0				0.2 L + R
	1.0	−0.8				L − 0.8 R
	−0.8	1.0				− 0.8 L + R
decoder matrix								decoded output

The procedure used to calculate this is found at the matrix multiplication page.

Definition 1: Complex numbers represent relative phase angles:

A reference signal x represented by +x.
A signal leading the reference signal x by 90° is represented by +j x.
A signal lagging the reference signal x by 90° is represented by −j x.
A signal at 180° from the reference signal x is represented by −x.
A signal at an odd angle θ is represented by x cos(θ) + x j sin(θ)

The rules of complex mathematics;

j can be treated as a variable in polynomial expressions.
+j × +1 = +j +j × +j = −1 +j × −1 = −j +j × −j = +1	+1 × +j = +j −j × −j = −1 −1 × +j = −j −j × +j = +1	−j × −j × −j = +j +j × +j × +j × −j = −1 +j × +j × +j = −j +j × +j × +j × +j = +1

Definition 2: The Poincaré Sphere
Groove Modulations

On Poincaré Sphere

The Poincaré Sphere was originally conceived by Henri Poincaré ("on-REE pwan-car-RAY") in 1892 to describe polarized light.

It is also called the Stokes Sphere, the Foucault Sphere, and the Fresnel Sphere.

Foucault ("foo-CO") used it to describe free-swinging pendulum motion.

Stokes and Fresnel ("freh-NELL") independently discovered its use for polarized light.

Scheiber and Robinson independently discovered its use in matrix quadraphonic signals.
The quadraphonic stylus motions are analogous to the Foucault pendulum motions.

The Poincaré Sphere represents the two channels of a stereo recording.

It represents stylus motions on a phonograph record, and signal relationships in other media.

The diagrams (right) are as follows:
- The upper diagram shows the stylus motions in the matrix quadraphonic phonograph record groove (as seen from the cartridge end of the tonearm).
  Note that the six fundamental orthogonal pairs are at right angles to each other or rotate in opposite directions.
- The lower diagram shows the Poincaré Sphere representations of these same stylus motions.
  Note that the six fundamental orthogonal pairs are dots on diametrically opposite sides of the sphere.
- The colors on each diagram show the six fundamental orthogonal pairs.
  The same color shows the same modulation in both diagrams.
  These colors apply to only these two diagrams.
These are the descriptions of the six orthogonal motions and their positions on the Poincaré Sphere:
- All modulations are on the surface of the sphere.
- The colors in this list apply to only these two diagrams.
- Points on the side of the sphere away from the viewer have large dots.
- Points on the near side of the sphere or on the limb have small dots.
- Lateral (horizontal or mono) stylus motion (0° phase) is at the right side of the sphere (olive) in this diagram
- Vertical stylus motion (180° phase) is at the left side of the sphere (violet).
- The left diagonal (left signal alone) is centered on the far side of the sphere (cyan).
- The right diagonal (right signal alone) is centered on the near side of the sphere (red).
- Clockwise motion (left signal leads right by 90°) is at the top of the sphere (black).
- Anticlockwise motion (right signal leads left by 90°) is at the bottom of the sphere (brown).

Definition 3: A great circle on the Poincaré Sphere

Great Circle

Any plane passing through the center of the Poincaré Sphere produces a great circle where it intersects the Poincaré Sphere.

The following matrix systems are examples of Great-Circle Matrix systems.

The order of the listed colors in the table shows the movement on this Poincaré sphere (shown at right) of a sound panned clockwise around the listener starting at the front.

Large spots are on the far side of the sphere.

MATRIX	ORIENTATION	COLORS ON DIAGRAM AT RIGHT
MATRIX	ORIENTATION	FRONT	RIGHT	BACK	LEFT	FRONT
QS, Stereo-4, Dynaquad	Equator	olive	red	violet	cyan	olive
UMX and BMX	Opposite Meridians	black	red	brown	cyan	black
BBC Matrix H (see below)	45° diagonal	tan	red	blue	cyan	tan
Matrix HR (see below)	45° opposite diagonal	pink	red	yellow	cyan	pink
Phase Location (Denon experiment)	Opposite Meridians	olive	brown	violet	black	olive

Most other matrix systems are not great-circle systems.

Postulate 3: The Poincaré Sphere can be used to represent the relative phase between any two signals:
The relative phase angles are as follows:
- The colors in this list apply to only the diagram at right.
- Points on the far side of the sphere have large dots, points on the near side of the sphere or on the limb have small dots.
- Lateral (horizontal or mono) is at the right of the sphere (olive); vertical (violet) is at the left.
- The left pole diagonal (cyan) is centered on the far side of the sphere.
- The right pole diagonal (red) is centered on the near side of the sphere.
- Clockwise motion (black) is at the top of the sphere, anticlockwise (brown) is at the bottom.
- Poincaré Sphere
  
  Corollary 1 to Postulate 3: Finding the great-circle distance between two points on the Poincaré Sphere:
  
  The following formula calculates the geodesic distance between two points on the surface of the sphere.
  
  This geodesic distance gives a central angle, which is used in the formulas below:
  
  The variables:
  - The poles are the L (cyan) and R (red) points on the sphere (see diagram).
  - The equator is the visible circle in the diagram.
  - The prime meridian crosses the equator at the 0° phase point (olive).
  - The first point has latitude φ1 has and longitude λ1
  - The second point has latitude φ2 has and longitude λ2
  - κ is the central angle along the equator.
  - σ is the central angle between the two points.
  - d is the length of the geodesic subtending the central angle.
  The calculations:
  - κ = |λ1 − λ2|
  - σ - arccos( sin(φ1) sin(φ2) + cos(φ1) cos(φ2) cos(κ) )
  - d = rσ (sigma is in radians)
  - Since the radius of the Poincaré Sphere is 1:
    d = σ (in radians), but is also the length of the geodesic arc.
Definition 4: Signals are said to be orthogonal (or to be an orthogonal pair) if they are located at opposite points (180° apart) on the Poincaré Sphere.
Examples of orthogonal pairs (see diagram above):
- Lateral stylus motion (olive) and vertical stylus motion (violet)
- The left diagonal (cyan) and the right diagonal (red)
- Clockwise motion (black) and anticlockwise motion (brown)
- Note that ANY pair of signals represented by points diametrically opposite on the Poincaré Sphere is an orthogonal pair.

Theorem 1: Any orthogonal pair on the Poincaré Sphere can be a pair of signals that can transmit the entire matrix quadraphonic program.

Proof for the following three orthogonal pairs:

The left diagonal (left channel) and the right diagonal (right channel):
These are the original left and right encoded channels, recorded in the left wall and the right of the stereo record groove using the Westrex 45/45 process.

Since no signal processing was done before making the recording, they are still the original unchanged L and R signals from the quadraphonic encoder.

L' = L R' = R

Lateral stylus motion and vertical stylus motion:

The created orthogonal signals are signals from a sum and difference matrix:
H = 0.71 L + 0.71 R	V = 0.71 L − 0.71 R
This orthogonal pair is used for FM multiplex stereo.
The original signals are recovered using a sum and difference matrix:
L' = 0.71 H + 0.71 V	R' = 0.71 H − 0.71 V
L' = 0.71 (0.71 L + 0.71 R) + 0.71 (0.71 L − 0.71 R)	R' = 0.71 (0.71 L + 0.71 R) − 0.71 (0.71 L − 0.71 R)
L' = 0.5 L + 0.5 R + 0.5 L − 0.5 R	R' = 0.5 L + 0.5 R − 0.5 L + 0.5 R
L' = L	R' = R

Clockwise stylus motion and anticlockwise motion

The created orthogonal signals are signals from a quadrature matrix:
A = 0.71 L + 0.71 Rj	B = 0.71 R + 0.71 Lj
The original signals are also recovered using a quadrature matrix:
L' = 0.71 A − 0.71 Bj	R' = 0.71 B − 0.71 Aj
L' = 0.71 (0.71 L + 0.71 Rj) − 0.71j (0.71 R + 0.71 Lj)	R' = 0.71 (0.71 R + 0.71 Lj) − 0.71j (0.71 L + 0.71 Rj)
L' = 0.5 L + 0.5 Rj + 0.5 L − 0.5 Rj	R' = 0.5 R + 0.5 Lj + 0.5 R − 0.5 Lj
L' = L	R' = R

In the general case, the recovery equations are always the complex conjugate of the pair-creating equations.

Theorem 2: If program material covers the entire Poincaré Sphere, then it is impossible to recover from that material a monophonic signal that contains all of it.
Proof: Any monophonic signal taken from 2-channel program material must be at some location on the Poincaré Sphere.

Because of this, any material at the point orthogonal to the point used must completely disappear from the monophonic signal.
- The left channel and right channel:
  The usual way to create a mono signal from a stereo signal is to use this sum:
  
  M = 0.71 L + 0.71 R
  
  But the following signal is entirely absent from the mono signal:
  
  0.71 L - 0.71 R
- The mono reconstruction Sansui used for mono playback of a QS record:
  Sansui used the sum of all of the decoder outputs, which reproduced the clockwise stylus motion and other motions that put sound into the clockwise reproduction
  
  The anticlockwise stylus motion (not usually used) fully disappears from this signal.
- This cancellation does not fully occur in a surround field (below) because every sound is picked up by several mics with different delays.
  At least one version of each sound will be picked up at an angle where it will be plainly decoded.

Theorem 3: The separation between two points on the Poincaré Sphere is calculated using the cosine of half the included angle.

The following are true of any two points on the Poincaré Sphere:

The straight line connecting any two points on the sphere is a chord.
The diagram at right is a plane passing through two pairs of points on the sphere for separation measurement and the center of the sphere.
The length of a chord of a circle is 2 r sin(θ/2) for radius r and subtended angle θ.
The radius r of the Poincaré Sphere is 1.

Poincaré Sphere Separations

Example 1:

Points A and B are the two points to be calculated.
Line segment AB is a chord subtending ∠α.
length(AB) = 2 sin(α/2)
length(AC) = sin(α/2)
Δ ACO is a right triangle with ∠COA = α/2.
length(CO) / length(AO) = cos(α/2)
Because hypotenuse AO has length 1, cos(α/2) = length(CO)
length(CO) is the crosstalk between A and B
- Note that when ∠α is 0°, cos(α/2) = 1.

- Note that when ∠α is 180°, cos(α/2) = 0.
The separation between points A and B is 20 log10(cos(α/2)).

Example 2:

Points Z and Y are the two points to be calculated.
Line segment ZY is a chord subtending ∠β.
length(ZY) = 2 sin(β/2)
length(ZX) = sin(β/2)
Δ ZXO is a right triangle with ∠XOZ = β/2.
length(XO) / length(ZO) = cos(β/2)
Because hypotenuse ZO has length 1, cos(β/2) = length(XO)
length(XO) is the crosstalk between A and B
- Note that when ∠β is 0°, cos(β/2) = 1.

- Note that when ∠β is 180°, cos(β/2) = 0.
The separation between points Y and Z is 20 log10(cos(α/2)).

Here are some of the commonly used values:

Sphere Angle	0	30	39	45	54	60	82	90	109	120	133	135	143	150	151	160	169	176	179	180
Crossfeed	1.00	0.97	0.94	0.92	0.89	0.87	0.75	0.71	0.58	0.50	0.40	0.38	0.32	0.26	0.25	0.18	0.10	0.03	0.01	0.00
Separation dB	0.0	-0.3	-0.5	-0.7	-1.0	- 1.2	- 2.5	-3.0	-4.7	-6.0	-8.0	-8.3	-10.0	-11.7	-12.0	-15.0	-20.0	-30.0	-40.0	-60.0

Corollary 1 to Theorem 3: The following separations can be calculated using this method:
- The separation between any two encoding points can be calculated from the positions of those points on the Poincaré Sphere.
- The separation between any two decoding points can be calculated from the positions of those points on the Poincaré Sphere:
  Front separation:
  - Between the left front and right front decoded positions
  Back separation:
  - Between the left back and right back decoded positions
  Front to back separation:
  - Between the left front and left back decoded positions
  - Between the right front and right back decoded positions
- The stereo playback separation of a quadraphonic recording can be calculated by finding the following separations:
  Front separation:
  - Between the left pole and the right front encoded position
  - Between the right pole and the left front encoded position
  Back separation:
  - Between the left pole and the right back encoded position
  - Between the right pole and the left back encoded position
- The quadraphonic playback of a stereo recording can be calculated by finding the following separations:
  Front separation:
  - Between the left pole and the right front decoded position
  - Between the right pole and the left front decoded position
  Back separation:
  - Between the left pole and the right back decoded position
  - Between the right pole and the left back decoded position
  Mono to back separation:
  - Between the mono (lateral) pole and the left back decoded position
  - Between the mono (lateral) pole and the right back decoded position
- The separation between any encoding point and any decoding point can be calculated from their positions on the Poincaré Sphere.
- The mono playback of any quadraphonic recording can be calculated by finding the following separations:
  Back attenuation:
  - Between the mono (lateral) pole and the center back encoded position
  - Between the mono (lateral) pole and any other encoded point
  Any position attenuated more than 10 dB effectively disappears from mono playback.
Here are separations calculated using these methods.

Calculation 1: Calculate the crosstalk between A and B from positions A and B on the Poincaré Sphere:
Procedure:
1. Divide the subtended angle between A and B by 2.
2. Find the cosine of the result.
C = cos(α/2)
Calculation 2: Calculate the separation between A and B in dB from the crosstalk between A and B:
Procedure:
1. Take the common logarithm of the crosstalk.
2. Multiply the result by 20.
S = 20 log10(C)
Calculation 3: Calculate the separation between A and B in dB from positions A and B on the Poincaré Sphere:
Procedure:
1. Divide the subtended angle between A and B by 2.
2. Find the cosine of the result.
3. Take the common logarithm of the new result.
4. Multiply the newest result by 20.
S = 20 log10(cos(α/2))
Calculation 4: Calculate the crosstalk between A and B from the separation between A and B in dB:
Procedure:
1. Divide the separation in dB by 20.
2. Raise 10 to the power of the result.
C = 10^(S/20)
Calculation 5: Calculate positions A and B on the Poincaré Sphere from the crosstalk between A and B:
Procedure:
1. Find the arc cosine of the crosstalk.
2. Multiply the result by 2.
α = 2 arccos(C)
Calculation 6: Calculate positions A and B on the Poincaré Sphere from the separation between A and B in dB:
Procedure:
1. Divide the separation in dB by 20.
2. Raise 10 to the power of the result.
3. Find the arc cosine of the new result.
4. Multiply the newest result by 2.
α = 2 arccos(10^(S/20))
Calc on Sphere

Calculation 7: Calculate L and R signal outputs to encode a desired position C on the Poincaré sphere:

The colors in this list apply to only the diagram at right.

The angle θ (theta) is the angle from the L pole (cyan) of the sphere to the desired point C.

The angle θ is also the angle from the R pole (red) of the sphere to the corresponding desired point C'.

C' is 180°-θ from the L pole.

The angle ø (phi) is the phase angle between L and R on the equator of the sphere, where:
- 0° is where L and R are in phase (olive).
- 90° is where L leads R by 90° (+j or black)
- 180° is where L is in opposite phase to R (violet)
- -90° is where L lags R by 90° (-j or brown)
The angle ρ (rho) is a phase shift added so the encoded signal has a wanted phase relationship to other signals.

The angles are converted into encoding sine-cosine variable pairs:
- a = cos(θ/2) b = sin(θ/2)
- f = cos(ø) - j sin(ø)
- t = cos(ρ) + j sin(ρ)
The left-side left and right encoding outputs for point C, using signal x, is:

L = atx R = bftx

The corresponding mirror-image right-side left and right encoding outputs for point C', using signal y, is:

L = bfty R = aty
Calculation 8: Calculate a mix of L and R signals to decode a desired position D on the Poincaré sphere:
Obtain the same angles used in the encoding equations above.

The angle θ (theta) is the angle from the L pole (cyan) of the sphere to the desired point D.

The angle θ is also the angle from the R pole (red) of the sphere to the corresponding desired point D'.

D' is 180°-θ from the L pole.

The angle ø (phi) is the phase angle between L and R on the equator of the sphere, where:

The angle ρ (rho) is a phase shift added so the encoded signal has a wanted phase relationship to other signals.

The angles are converted into decoding sine-cosine variable pairs:
- a = cos(θ/2) b = sin(θ/2)
- f = cos(ø) + j sin(ø)
- t = cos(ρ) - j sin(ρ)
The decoding output for point D, using signals L and R, is:

U = atL + bftR

The corresponding mirror-image decoding output for point D', using signals L and R, is:

V = bftL + btR

Theorem 4: To decode original encoding points, decode equations must use complex conjugates of encode equations.

In these equations, a, b, c, and d are values between -1 and 1.

In these equations, s and t are sign values of +1 or -1. Variable s goes with X, and t goes with Y.

In these equations, u and v are sign values of +1 or -1. Variable u goes with L, and v goes with R.

In these equations, m and n are sign values of +1 or -1. Variable m goes with Lj, and v goes with Rj.

For the encoding of any pair of symmetric signals, the following equations are used:

L = u(saX + smbXj + tcY + tmdYj)
R = v(taY + tnbYj + scX + sndXj)

For the decoding of any pair of symmetric signals, the following equations are used:

X = s(uaL - umbLj + vcR - vndRj)
Y = t(vaR - vnbRj + ucL - umdLj)

Examples include the following matrix systems:

Sansui QS:

PAIR	a	b	c	d	s	t	u	v	m	n
lf and rf	0.92	0.00	0.38	0.00	+1	+1	+1	+1	+1	+1
lb and rb	0.00	0.92	0.00	0.38	+1	+1	+1	-1	+1	+1

Encoding equations:

L = .92lf + .38rf + .92lbj + .38rbj
R = .92rf + .38lf - .92rbj - .38lbj

Decoding equations:

lf = .92L + .38R
rf = .38L + .92R
lb = -.92Lj + .38Rj
rb = -.38Lj + .92Rj

CBS SQ:

PAIR	a	b	c	d	s	t	u	v	m	n
lf and rf	1.00	0.00	0.00	0.00	+1	+1	+1	+1	+1	+1
lb and rb	0.00	0.71	0.71	0.00	-1	+1	+1	+1	+1	+1

Encoding equations:

L = lf - .71lbj + .71rb
R = rf - .71lb + .71rbj

Decoding equations:

lf = L
rf = R
lb = .71Lj - .71R
rb = .71L - .71Rj

BBC Matrix H:

PAIR	a	b	c	d	s	t	u	v	m	n
lf and rf	0.85	0.35	0.35	0.15	+1	+1	+1	+1	+1	-1
lb and rb	0.35	0.85	0.15	0.35	+1	+1	+1	+1	-1	+1

Encoding equations:

L = .85(lf - lbj) + .35(lfj + rf + lb - rbj) + .15(rfj + rb)
R = .85(rf + rbj) + .35(lf - rfj + lbj + rb) - .15(lfj - lb)

Decoding equations:

lf = .85L - .35(Lj - R) + .15Rj
rf = .85R + .35(L + Rj) - .15Lj
lb = .85Lj + .35(L - Rj) + .15R
rb = -.85Rj + .35(Lj + R) + .15L

Note the following special values in the above matrices:

0.92 = cos(22.5°)
0.38 = cos(67.5°)
0.71 = cos(45.0°)
0.15 = cos(67.5°) × cos(67.5°)
0.35 = cos(67.5°) × cos(22.5°)
0.85 = cos(22.5°) × cos(22.5°)

Theorem 5: It is impossible to pan a signal all the way around any great circle on the Poincaré Sphere without encountering a phase discontinuity (usually called a hole).

No matter which great-circle matrix is used, there is at least one point where panning must be interrupted for a phase change as the sound is panned completely around the listener:

No matter which great circle is used, either the phase is continually changed as the signal is panned, or the phase must be changed at some point.

If all of the phase changes are at zero crossings, then the final phase of the signal after the panning will be reversed from the original signals before the panning, as shown here:

Phase reversal without hole:

DIR	F	RF	R	RB	B	LB	L	LF	F
L	0.71	0.38	0.00	−0.38	−0.71	−0.92	−1.00	−0.92	−0.71
R	0.71	0.92	1.00	0.92	0.71	0.38	0.00	−0.38	−0.71

Examples of systems with planned holes:

Scheiber, Dynaquad, Stereo-4:

The red bar shows the encoding phase hole:

DIR	F	RF	R	RB	B		B	LB	L	LF	F
L	0.71	0.38	0.00	−0.38	−0.71		0.71	0.92	1.00	0.92	0.71
R	0.71	0.92	1.00	0.92	0.71		−0.71	−0.38	0.00	0.38	0.71

Uniquad Mixer-Bus RM Encoding:

The orange bars are where the bus selector is changed when panning:

DIR	F	RF	R		R	RB	B	LB	L		L	LF	F
L	0.71	0.38	0.00		−0.00	−0.38	−0.71	−0.92	−1.00		1.00	0.92	0.71
R	0.71	0.92	1.00		1.00	0.92	0.71	0.38	0.00		0.00	0.38	0.71

Sansui QS:

The orange bars show the encoding phase holes, automatically adjusted by phasors in the encode equations:

DIR	F	RF	R		R	RB	B	LB	L		L	LF	F
L	0.71	0.38	0.00		0.00j	0.38j	0.71j	0.92j	1.00j		1.00	0.92	0.71
R	0.71	0.92	1.00		−1.00j	−0.92j	−0.71j	−0.38j	−0.00j		0.00	0.38	0.71

Denon BMX:

The orange bars show the encoding phase holes. It is unknown how they were implemented in practice:

DIR	F	RF	R	R	RB	B	LB	L	L	LF	F
L	0.50	0.26	0.00	0.00	0.26	0.50	0.65	0.71	0.71	0.65	0.50
Lj	0.50j	0.26j	0.00j	−0.00j	−0.26j	−0.50j	−0.65j	−0.71j	0.71j	0.65j	0.50j
R	0.50	0.65	0.71	0.71	0.65	0.50	0.26	0.00	0.00	0.26	0.50
Rj	−0.50j	−0.65j	−0.71j	0.71j	0.65j	0.50j	0.26j	0.00j	−0.00j	−0.26j	−0.50j

Most matrix systems that are not great circle matrix systems also have at least one point where panning must be interrupted for a phase change as the sound is panned completely around the listener.

Theorem 6: Different matrix definitions use different coefficients to define the same matrix encodings. The coefficients differ only in total level.

To go from one definition to another, multiply all coefficients by the same value.

Example: Scheiber system and Sansui QS:

Value	Original system	×	Resulting System	Value	Original system	×	Resulting System
System	Scheiber		QS	System	QS		Scheiber
Major Value	0.92	× 1.08 =	1.00	Major Value	1.00	× 0.92 =	0.92
Minor Value	0.38	× 1.08 =	0.41	Minor Value	0.41	× 0.92 =	0.38
Resultant Value	1.00	× 1.08 =	1.08	Resultant Value	1.08	× 0.92 =	1.00

The procedure to find out what to multiply the original system coefficients by to get the resulting system is:

Find which coefficient in the original system has the value 1.00.
Use the coefficient for the same value from the resulting system as the multiplier.

The following table shows the same matrix encoding in several different ways:

Percent Blend	Major is 1.00		Result is 1.00		Encode Angle
Percent Blend	Minor	Result	Major	Minor	Stylus θ
100%	1.00	1.41	0.71	0.71	45.0°
80%	0.80	1.28	0.78	0.62	38.7°
50%	0.50	1.12	0.89	0.46	26.6°
41%	0.41	1.08	0.92	0.38	22.5°
32%	0.32	1.05	0.95	0.30	22.5°
30%	0.30	1.04	0.96	0.29	16.7°
25%	0.25	1.03	0.97	0.24	14.0°
20%	0.20	1.02	0.98	0.20	11.3°

Each row is the same matrix encoding, shown using different coefficients.

Definition 5: A set of matrix coefficients where all of the resultant values are exactly one shall be referred to as a normalized set of coefficients.

A matrix with normalized coefficients will not cause any change of total level to signals passing through it.

Matrix quadraphonic systems analyzed mathematically and geometrically:

PUTTING IT ALL TOGETHER

Input Values			ΔXEF (XE=1)					Angle		ΔXDO (XO=1)		Poincaré Sphere (r = 1)					Sphere Separation			Stylus Motion
Matrix used with	% Blend	dB	tan(θ) FE opp	sec(θ) XF hyp	xsc(θ) OF hyp	csc(θ) XC hyp	xsc(θ) BC hyp	∠EXF ZXY θ	∠ZOY 2θ	cos(θ) XD adj	sin(θ) OD opp	∠XOZ α	XZ Chord	OD ⊥ XZ Chord	OM ⊥ YZ Chord	OU ⊥ VW Chord	OD dB	OM dB	OU dB	to opp chan ∠PXE	to adj chan ∠AXE
Calc:	bl %	vdB	= bl	sec(θ)	XF-1	csc(θ)	XC-1	atn(FE)	2θ	cos(θ)	sin(θ)	180-2θ	2sin(α/2)	cos(α/2)	cos(θ)	sin(2θ)	vdB	vdB	vdB	90-θ	θ
SQ-b,HA-b	100.0	0.0	1.000	1.414	0.414	1.414	0.414	45.0	90.0	0.707	0.707	90.0	1.414	0.707	0.707	1.000	-3.01	-3.01	0.00	45.0	45.0
EV4-bd	80.0	-1.9	0.800	1.281	0.281	1.601	0.601	38.7	77.3	0.781	0.625	102.7	1.562	0.625	0.781	0.976	-4.09	-2.15	-0.21	51.3	38.7
Nar	67.0	-3.5	0.670	1.204	0.204	1.797	0.797	33.8	67.6	0.831	0.557	112.4	1.662	0.557	0.831	0.925	-5.09	-1.61	-0.68	56.2	33.8
Nar2	60.0	-4.4	0.600	1.166	0.166	1.944	0.944	31.0	61.9	0.857	0.514	118.1	1.715	0.514	0.857	0.882	-5.77	-1.34	-1.09	59.0	31.0
DQ-bd	57.7	-4.8	0.577	1.155	0.155	2.001	1.001	30.0	60.0	0.866	0.500	120.0	1.732	0.500	0.866	0.866	-6.03	-1.25	-1.25	60.0	30.0
EV4-be,DQ-be	50.0	-6.0	0.500	1.118	0.118	2.236	1.236	26.6	53.1	0.894	0.447	126.9	1.789	0.447	0.894	0.800	-6.99	-0.97	-1.94	63.4	26.6
QS,UM,H,HA-f	41.4	-7.7	0.414	1.082	0.082	2.614	1.614	22.5	45.0	0.924	0.383	135.0	1.848	0.383	0.924	0.707	-8.35	-0.69	-3.01	67.5	22.5
SQB-bd,EVU-bd	40.0	-8.0	0.400	1.077	0.077	2.693	1.693	21.8	43.6	0.928	0.371	136.4	1.857	0.371	0.928	0.690	-8.60	-0.64	-3.23	68.2	21.8
UQE	31.8	-10.0	0.318	1.049	0.049	3.300	2.300	17.6	35.3	0.953	0.303	144.7	1.906	0.303	0.953	0.578	-10.4	-0.42	-4.77	72.4	17.6
EV4-fe	30.0	-10.5	0.300	1.044	0.044	3.480	2.480	16.7	33.4	0.958	0.287	146.6	1.916	0.287	0.958	0.550	-10.8	-0.37	-5.19	73.3	16.7
DQ-fe	25.0	-12.0	0.250	1.031	0.031	4.123	3.123	14.0	28.1	0.970	0.243	151.9	1.940	0.243	0.970	0.471	-12.3	-0.26	-6.55	76.0	14.0
EV4-fd,EVU-fd	20.0	-14.0	0.200	1.020	0.020	5.099	4.099	11.3	22.6	0.981	0.196	157.4	1.961	0.196	0.981	0.385	-14.2	-0.17	-8.30	78.7	11.3
SQB-fd	10.0	-20.0	0.100	1.005	0.005	10.050	9.050	5.7	11.4	0.995	0.100	168.6	1.990	0.100	0.995	0.198	-20.0	-0.04	-14.0	84.3	5.7
Wide	5.0	-26.0	0.050	1.001	0.001	20.025	19.025	2.9	5.7	0.999	0.050	174.3	1.998	0.050	0.999	0.100	-26.0	-0.01	-20.0	87.1	2.9
DQ-fd	0.0	-80.0	0.000	1.000	0.000	99.000	98.001	0.0	0.0	1.000	0.000	180.0	2.000	0.000	1.000	0.000	-80.0	0.00	-80.0	90.0	0.0
Matrix	Blend	dB	FE	XF	OF	XC	BC	θ	2θ	XD	OD	α	XZ	OD	OM	OU	OD dB	OM dB	OU dB	∠PXE	∠AXE

Here are all of the items above put into one table.

The variables in the table are:

MATRIX COEFFICIENTS

USING ΔXEF

FE = the blending between the channels used to encode or decode
With Excel, I had to enter the % Blend value 0.0 as 0.01 to prevent #NUM! errors.
FE = tan(θ)
XE = the fixed unity value (1) the blend is added to
XF = sec(theta;) = the resultant sum of 1 and the blend
OF = xsc(theta;) = sec(θ) − 1 = the exsecant of θ
θ = the angle ∠EXF from the blend - the arctangent of FE/1
θ = ∠EXF = ∠AXE = ∠DXO

USING ΔCEX

CE = cot(θ)
XC = csc(θ)
BC = xcs(θ) = csc(θ) − 1 = the excosecant of θ

USING ΔXDO and ΔXAE

XD = XA = cos(θ) = calculate major coefficient and stylus vector
OD = EA = sin(θ) = calculate minor coefficient and stylus vector
OX = EX = the fixed unity value (1) for stylus motion resultants
These are the normalized coefficients.

TRIGONOMETRIC AND GEOMETRIC IDENTITIES

XE = OX = 1
FE = tan(θ) = sin(θ) / cos(θ)
XF = sec(θ) = 1 / cos(θ)
CE = cot(θ) = cos(θ) / sin(θ)
XC = csc(θ) = 1 / sin(θ)
XE = XB = OX = OZ = OY = OW = OV = 1
θ = ∠AXE = ∠DXO = ∠DZO = ∠MOZ = ∠MOY = ∠PEX
θ = ∠EXF = ∠ZXY = ∠PCE = ∠ECX = ∠XCF = ∠AEF
ΔAXE ≅ ΔDXO ≅ Δ;DZO ≅ Δ;MOZ ≅ Δ;MOY ≅ Δ;PEX
ΔEXF ∼ ΔAXE ∼ ΔZXY ∼ ΔPCE ∼ ΔECX ∼ ΔXCF ∼ ΔAEF

STYLUS VECTORS (Lower diagram for proper orientation to a record groove)

XA ≅ XD = actual major stylus vector (both diagrams)
EA ≅ OD = actual minor stylus vector (both diagrams)
EX ≅ OX = actual stylus resultant (=1 both diagrams))
ΔXDO ≅ ΔXAE ≅ ΔOMY ≅ ΔOMZ
ΔXAE (lower diagram) shows an encoding of a Regular Matrix right front signal.

POINCARÉ SPHERE VALUES

SPHERE ANGLES

∠ZOY = 2θ = 2(∠ZXY) ... Central angle theorem
∠XYZ ≅ ∠XFE ≅ ∠XOD ≅ ∠XEA
α = ∠XOZ = 180°-2θ = Sphere angle opposite
α/2 = 90°-θ
θ = 90°-α/2
FE = tan(θ) = blend

SPHERE ANGLE OPPOSITE

α = Sphere angle for encoded signal to opposite stereo channel
XZ = Sphere chord = tool for calculating opposite Sphere separation.
OD = Perpendicular bisector of XZ ... gives separation value of opposite sphere angle.
OD = EA = sin(θ) = Separation to opposite stereo channel.
OD in dB is found by multiplying the common logarithm of OD by 20.

SPHERE ANGLE ADJACENT

2θ = ∠YOZ = 180°-α = Sphere angle adjacent
∠YOZ = 2θ = Sphere angle for encoded signal to adjacent stereo channel
YZ = Sphere chord = tool for calculating adjacent Sphere separation.
OM = Perpendicular bisector of YZ and gives separation value of adjacent sphere angle.
OM = AX = cos(θ) = Separation to adjacent stereo channel.
OM in dB is found by multiplying the common logarithm of OM by 20.

SPHERE ANGLE CODED TO CODED

∠VOW = 180°-4θ = Sphere angle between left and right identically coded outputs
∠VOW = Sphere angle for coded signal to coded signal
VW = Sphere chord = tool for calculating coded Sphere separation.
OU = Perpendicular bisector of VW and gives separation value of sphere angle.
OU = sin(2θ) = cos(90°-2θ) = Separation between paired encoded or decoded channels.
OU in dB is found by multiplying the common logarithm of OU by 20.

CALCULATIONS FROM THE ABOVE FACTS

Calculation 9: Derive resistors for an output of L and R signals to matrix encode a desired position (diagram 1):
- Two resistors, G and F, form a voltage divider for the major side of encoding.
  Two more resistors, H and F, form another voltage divider for the minor side.
  The page author used a 1K ohm at 1/8 watt for resistor F.
- G = 1K (xsc(θ)) = 1K (sec(θ) − 1) = 1K ((1 ⁄ cos(θ)) − 1) H = 1K (xcs(θ)) = 1K (csc(θ) − 1) = 1K ((1 ⁄ sin(θ)) − 1)
- The phase of either signal can be changed before this mixer. The decode angle is θ from the table above.

Calculation 10: Derive resistors for an output of L and R signals to matrix decode a desired position (diagram 2):

Two resistors, A and B, form a mixer to matrix decode a channel. The page author used a 1K ohm resistor at 1/8 watt for resistor A.
B = 1K (cot(θ)) = 1K (1 ⁄ tan(θ))
The phase of either signal can be changed before this mixer. The decode angle is θ from the table above.

Calculation 11: Derive resistors for a mix of L and R signals to matrix decode a desired channel (diagram 2):
- Two resistors, A and B, form a mixer to matrix decode a channel. The page author used a 10K ohm sum at 1/8 watt.
- A = 10K (cos(θ) ⁄ (cos(θ) + sin(θ)) B = 10K (sin(θ) ⁄ (cos(θ) + sin(θ)) are the decode resistors.
- The phase of either signal can be changed before this mixer. The decode angle is θ from the table above.
Calculation 12: Derive a potentiometer setting for a mix of L and R signals to matrix decode a desired channel (diagram 3):
- A potentiometer P is the matrix parameter control and mixer. The page author used 10K ohms at 2 watt.
- T = P (cos(θ) ⁄ (cos(θ) + sin(θ)) is the decode setting of the tap.
- The phase of either signal can be changed before this mixer. The decode angle is θ from the table above.
Calculation 13: Derive resistors for a blend of L and R signals to encode or decode a desired matrix blend coefficient (diagram 4):
- Two fixed input resistors ɪ achieve the blend. The page author used 1K ohms at 1/8 watt.
- A potentiometer W is the Width control. It should be at least 15 × ɪ. The page author used 20K ohms at 2 watt.
- W = (ɪ ⁄ width_factor) − ɪ is the width setting. W = (1000 ⁄ width_factor) − 1000 is the page author's setting.
- The phase of either signal can be changed before this mixing. The width_factor is tan(θ) from the table above.
Calculation 14: Derive resistor for a blend of L and R signals to decode a desired speaker matrix width coefficient (diagram 4):
- Two fixed input resistors ɪ achieve the blend. The page author used 3 ohms at amplifier power.
- A rheostat W is the Width control. It should be at least 15 × ɪ. The page author used 50 ohms at amplifier power.
- W = (ɪ ⁄ width_factor) − ɪ is the width setting. W = (3 ⁄ width_factor) − 3 is the page author's setting.
- The width_factor is tan(θ) from the table above.
Calculation 15: Derive resistor for an antiblend of L and R signals to decode a desired speaker matrix depth coefficient (diagram 5):
- The speakers themselves are the input resistances S. The page author used his 8-ohm speakers, so S is 8 ohms.
- A rheostat is the Depth control D. Its resistance should be at least 6 × S. The page author used 50 ohms at amplifier power.
- D = (S ⁄ (1 − depth_factor)) − S is the depth setting. D = (8 ⁄ (1 − depth_factor)) − 8 is the page author's setting.
- The depth_factor is tan(θ) from the table above.

Features of matrix quadraphonic systems:

Theorem 7: A surround field uses level and time differences between channels to locate the sound, using sound location properties of the human hearing system.

Hans Wallach, Edwin Newman, and Mark Rosenzweig defined the precedence effect in 1949. Helmut Haas later investigated the subject more in 1949.

They showed that when a sound reaches the ears, followed by an identical sound from a different direction, the listener hears only one sound where the first sound came from.

The delay between the sounds can be as long as:
- 5 ms for clicks (sound travels about 5.5 feet)
- 40 ms for complex sounds (speech or music - sound travels about 45 feet).
Larger delays are heard as echoes.

Human hearing uses these time and level differences in sounds reaching each ear to indicate the direction each sound comes from.

A special microphone array is used to create a surround field.

It encodes a quadraphonic matrix signal with the time delays already included to give additional clues to correctly locate the sound.

No separation enhancement is needed in playback.

Surround field page

Why surround fields work

Here is a table of the relative levels and delays (in microseconds) received on the input microphones l, r, and s of such a recording for different directions of sound sources:

Angle	Level l	Delay l	Level r	Delay r	Level s	Delay s	Direction	1st	2nd	3rd
0	0.866	0	0.866	0	~ 0.200	885	Straight Ahead	l r	s
30	0.707	369	0.966	0	0.259	951		r	l	s
60	0.500	639	1.000	0	0.500	762	Right Mic	r	l s
90	0.259	737	0.966	0	0.707	369	Straight Right	r	s	l
120	~ 0.200	762	0.866	123	0.866	0		r s	l
180	0.500	885	0.500	885	1.000	0	Straight Back Mic	s	l r
240	0.866	123	~ 0.200	762	0.866	0		l s	r
270	0.966	0	0.259	737	0.707	369	Straight Left	l	s	r
300	1.000	0	0.500	639	0.500	762	Left Mic	l	r s
330	0.966	0	0.707	369	0.259	951		l	r	s
360	0.866	0	0.866	0	~ 0.200	885	Straight Ahead	l r	s

~ Approximate value - Spill sound from room reflections into mics.

The stereo recording is matrixed from these three channels:

L = 0.98 l + 0.20 r - 0.71 s
R = 0.98 r + 0.20 l + 0.71 s

Decoding works with Dolby Surround or with any regular matrix (RM or QM) decoder.

Notice that this idea works only with a great-circle matrix. It won't work with phase matrix systems.

Observation 1: The separations the listeners notice the most
The separations in a quadraphonic program that the listener notices the most are:
1. Left front to right front
2. Center front to center back
The other separations are not as noticeable. The separation between left back and right back is usually the least noticed.

SIDE LOCATION AND SEPARATION ENHANCEMENT:

Observation 2: The Side-Location problem -
Two speakers placed left-front and left-back of the listener can't produce a sound image between them when a sound is panned between them.
(This occurs on the right side too.)
Normal level-differential panning techniques cannot produce an audible image between these speakers
unless the listener turns his head so that one each ear is facing each speaker.
But there are several ways to make the side image appear, and some of them use normal panning techniques when the recording is mixed:
1. Speakers directly to the left side and the right side of the listener
  Any surround sound system with speakers located directly to the left and directly to the right of the listener does not have the side-location problem.
  
  - The Dynaco Diamond has these speakers and unintentionally fixed this problem.
  
  - The Denon QX Dual Triphonic system also unintentionally fixed this problem.
2. Diagonal Delays
  This method uses the precedence effect to make the separations seem larger.
  It introduced a phase-reversed and delayed version of each decoded channel into the diagonally opposite channel.
  
  - It did increase the apparent separation.
  
  - It fixed the side location problem.
  
  - It also caused an annoying tension feeling from phase reversed sound.
3. Binaural recording.
  This uses microphones spaced the same distance apart that human ears are spaced. The microphones are aimed to the sides.
  
  The listener listens to a recording from those microphones through earphones.
  
  The effect is very real, but there is no sound from the front or the back even if such sounds were there.
  
  The effect is also audible with speakers.
  
  Quadraphonic speakers using an RM or QM matrix will place the images between the side speakers with the listener's head facing the front.
  
  This places images between the speakers, but does not produce a quadraphonic recording.
4. Delayed back channels
  Dolby Surround plays a normally matrixed Dolby Surround, RM, or QM recording, decoding the dialog, left, right, and surround channels.
  
  The surround channels are delayed by the decoder to prevent surround leakage into the front from being noticed.
  
  But this delay also uses the precedence effect to cause the side images to be located by the listener correctly as it was panned.
  
  - It requires the listener to continue facing forward to hear all of the location effects correctly.
5. Enhancement in the Recording
  This method uses the precedence effect to make the separations seem larger.
  
  The difference is that it is in the recording. Nothing is added to the decoding equipment.
  
  This is a surround (or Spheround) version of binaural recording.
  
  It has delays in both left-right and front-back directions (and up-down directions too for Spheround).
  
  So the position of the listener's head is unimportant.
  
  - A special microphone technique creates a sound field. The human hearing system does the rest.
  
  - Surround field page
  
  - Why surround fields work
  
  - This is like binaural recording, but works in a plane or even a solid space.
  
  - It increases the apparent separation.
  
  - No other separation enhancement is needed.
  
  - It fixes the side-location problem.
  
  - It gives a natural "you are there" effect that is a characteristic of sound fields.
6. Many Channels
  The effect here is having so many channels that at least one or two pairs of channels are at opposite sides of the listener's head. This removes the side-location problem.
  
  The Octophonic system works well.
  
  How Octophonics fix the side-location problem.
7. Faking surround fields
  This method uses the precedence effect to make the separations seem larger.
  It introduces a delayed version of each decoded channel into the diagonally opposite channel or to other speakers nearby but farther away.
  
  The phase is not reversed as it is in the Diagonal Delays above.
  
  - It does increase the apparent separation.
  
  - It fixes the side location problem.
  
  - It does not cause the annoying tension feeling from phase reversed sound.
  
  - These speakers do not have to be exactly diagonally opposite. They just need to be heard by the opposite ear.

Definition 5: Separation Enhancement - A method to make the separation of a matrix system seem larger than it really is.

There are several different methods:

Gain Riding
In this method, the gain of each channel is quickly varied to make the dominant channels louder and the other channels quieter.
This seemed to make the separation larger, but it had two disadvantages:

- It reduced the level of any ambience in the recording.

- It had the effect of "pumping" (where changes in signal levels or ambience caused by gain changes are noticed by the listener).
Diagonal Delays
This method uses the precedence effect to make the separations seem larger.
It introduced a phase-reversed and delayed version of each decoded channel into the diagonally opposite channel.

- It did increase the apparent separation.

- It fixed the side location problem.

- It also caused an annoying tension feeling from phase reversed sound.

Automatic Matrix Varying

This method is used in the Sansui Variomatrix, the CBS Variblend, Dolby Pro-Logic, the Electro-Voice separation enhancement, and UniQuad Autovary.

- This looks for where the strongest signal is and momentarily adjusts the matrix to increase separation for that signal.

- The reduced separations for the other channels are not normally noticed.

- The upper diagram shows the normal separation pattern for Dolby Surround.

- The lower diagram shows the instantaneous changes Dolby Surround makes with a dominant front-center soloist.

- Decoding moves away from dominant sources. Front separation widens while back separation narrows with front-center solos.

DECODE EQUATIONS		DECODE RESULTS
Without Pro-Logic
Left_Speaker	= 1.00 Left_Matrix	Left_Speaker	= 1.00 Left + .707 Dialog + .707 j Surround
Right_Speaker	= 1.00 Right_Matrix	Right_Speaker	= 1.00 Right + .707 Dialog - .707 j Surround
Dialog_Speaker	= .707 Left_Matrix + .707 Right_Matrix	Dialog_Speaker	= 1.00 Dialog + .707 Left + .707 Right
Surround_Speaker	= .707 Right_Matrix - .707 Left_Matrix	Surround_Speaker	= 1.00 Surround + .707 Left - .707 Right
With Pro-Logic (front solo)
Left_Speaker	= .924 Left_Matrix - .383 Right_Matrix	Left_Speaker	= .924 Left + .383 Dialog + .924 j Surround
Right_Speaker	= .924 Right_Matrix - .383 Left_Matrix	Right_Speaker	= .924 Right + .383 Dialog - .924 j Surround
Dialog_Speaker	= .707 Left_Matrix + .707 Right_Matrix	Dialog_Speaker	= 1.00 Dialog + .707 Left + .707 Right
Surround_Speaker	= .707 Right_Matrix - .707 Left_Matrix	Surround_Speaker	= 1.00 Surround - .707 Left - .707 Right

Pumping is inaudible using this method because the signal levels are unchanged.
Only the instantaneously perceived directions of the low level signals are changed.
These are not normally noticed because human hearing normally notices the direction of the dominant signal over the other signals.

Delayed back channels
Dolby Surround plays a normally matrixed Dolby Surround, RM, or QM recording, decoding the dialog, left, right, and surround channels.

The surround channels are delayed by the decoder.

This delay prevents surround leakage into the front from being noticed.

This delay prevents front leakage into the surround channels from being noticed.

This delay also uses the precedence effect to cause the side images to be located correctly as panned by the listener.

- It requires the listener to continue facing forward to hear all of the location effects correctly.
Enhancement in the Recording
This method uses the precedence effect to make the separations seem larger. The difference is that it is in the recording. Nothing is added to the decoding equipment.

See "Theorem 7: Surround Fields" above and the Surround Fields page.

- A special microphone technique creates a sound field. The human hearing system does the rest.

- Why surround fields work

- It increases the apparent separation.

- No other separation enhancement is needed.

- It fixes the side-location problem.

- It gives a natural "you are there" effect that is a characteristic of sound fields.
Many Channels
Each sound comes from a wall of sound, not a single point. This does the following:
- It makes it useful from more locations in the room.
- It creates a linear wave front instead of multiple spherical wave fronts.
- It keeps the ears from finding a single speaker in the room.
Thus, the ears locate the correct direction of the sound as panned.

The Octophonic system

How Octophonics enhance separation
Faking surround fields
This method uses the precedence effect to make the separations seem larger.
It introduces a delayed version of each decoded channel into the diagonally opposite channel or to other speakers nearby but farther away.

The phase is not reversed as it is in the Diagonal Delays above.

- It does increase the apparent separation.

- It fixes the side location problem.

- It does not cause the annoying tension feeling from phase reversed sound.

- These speakers do not have to be exactly diagonally opposite. They just need to be heard by the opposite ear.

SOUND IMAGE DIAGRAMS:

Definition 6: Sound Image Diagram - A diagram showing the size and shape of the total sound image of a quadraphonic system.

This procedure was developed by the page author through empirical experimentation. But it seems to work very well:

The page author wanted to create a diagram of room size as shown in Leonard Feldman's book "Four Channel Sound" on page 62.

Diagram calculations

He started with separation figures in dB for the various systems.

Value A	Separation between front channels
Value B	Separation between back channels
Value C	Separation between front and back channels on each side
Value D	Separation between each front channel and the opposite stereo channel
Value E	Separation between each back channel and the opposite stereo channel
Value F	Separation between each back channel and a mono signal
Value G	Separation between the center back signal and a mono signal
Value H	Separation between each front channel and the center back channel
Value K	Separation between each front channel and the opposite back channel
Value S	Normal stereo separation of the record (assumed 40 dB)
Value T	Separation between a stereo channel and mono (3 dB)
Value U	Separation between a stereo channel and the center back signal

For values of 0 dB, he had to use 0.05 dB to keep Excel from giving an error.

Next he created a linear version of a separation indication.

He took the common logarithm of each of the dB values above.

This gave a scale of values from -1.3 to 1.6 for values from .05 dB to 40 dB.

He then centered the values by subtracting 0.5 from each value for the final effect.

This gave a scale of values from -1.8 to 1.1 for values from .05 dB to 40 dB.

This would expand the space for large separations while contracting it for small ones. It also gave the wanted appearance.

Matrix	A	B	C	D	E	F	G	H	K	S	T	U
QS	3	3	3	8.3	8.3	8.3	40	8.3	40	40	3	3
	-0.02	-0.02	-0.02	0.42	0.42	0.42	1.10	0.42	1.10	1.10	-0.02	-0.02
EV4	8.3	0.2	4.9	14	4.1	19	40	5.1	5.3	40	3	3
	0.42	-1.2	0.19	0.65	0.11	0.78	1.10	0.21	0.22	1.10	-0.02	-0.02

He then created a framework to put these in:
This frame is a 4-unit by 4-unit square centered on the origin of the graph.

This plot area is an 8-unit by 8-unit box centered on the origin of the graph.

W is the width at the front. Y is the width at the back.
X is the depth at the front. Z is the depth at the back.

He then empirically found equations to represent the effects the above separations have on the image:

LOCATION	DIRECTION	SAME SIDE	LET	OPP INPUT	LET	DIAGONAL	LET	MIRROR	OFFSET	FORMULA
COEFFICIENTS:			1.0		0.1		0.01		+2
Right Front	Horizontal	Left Front	A	Left Input	D	Left Back	K	Left Front	+2	'W = 1.0 A + 0.1 D + 0.01 K + 2
Left Front	Horizontal	Right Front	A	Right Input	D	Right Back	K	Right Front	+2	'-W = -1.0 A - 0.1 D - 0.01 K - 2
Right Front	Vertical	Right Back	C	Center Back	H	Left Back	K	Left Front	+2	'X = 1.0 C + 0.1 H + 0.01 K + 2
Left Front	Vertical	Left Back	C	Center Back	H	Right Back	K	Right Front	+2	'X = 1.0 C + 0.1 H + 0.01 K + 2
Right Back	Horizontal	Left Back	B	Left Input	E	Left Front	K	Left Back	+2	'Y = 1.0 B + 0.1 E + 0.01 K + 2
Left Back	Horizontal	Right Back	B	Right Input	E	Right Front	K	Right Back	+2	'-Y = -1.0 B - 0.1 E - 0.01 K - 2
Right Back	Vertical	Right Front	C	Mono	F	Left Front	K	Left Back	+2	'Z = -1.0 C - 0.1 F - 0.01 K - 2
Left Back	Vertical	Left Front	C	Mono	F	Right Front	K	Right Back	+2	'Z = -1.0 C - 0.1 F - 0.01 K - 2

A second set was needed for diamond speaker layouts:

LOCATION	DIRECTION	SAME SIDE	LET	OPP INPUT	LET	DIAGONAL	LET	MIRROR	OFFSET	FORMULA
COEFFICIENTS:			1.0		0.1		0.1		+2
Front	Horizontal	0								'W = 0
Back	Horizontal	0								'W = 0
Front	Vertical	Back	G	Left Input	T	Right Input	T	Back	+2	'X = 1.0 G + 0.1 T + 0.1 T + 2
Back	Vertical	Front	G	Left Input	U	Right Input	U	Front	+2	'-X = -1.0 G - 0.1 U - 0.1 U - 2
Right	Horizontal	Left	S	Mono	T	Back	U	Left	+2	'Y = 1.0 S + 0.1 T + 0.1 U + 2
Left	Horizontal	Right	S	Mono	T	Back	U	Right	+2	'-Y = -1.0 S - 0.1 T - 0.1 U - 2
Right	Vertical	0								'Z = 0
Left	Vertical	0								'Z = 0

The final step was to get Excel to make the diagrams:

Provide a table row for the x coordinates and a row for the y coordinates

The points are in the order lb, lf, rf, rb, lb (for diamond pattern: l, f, r, b, l).

The lb point is repeated to complete the quadrilateral (repeat l for the diamond pattern).

Use the plot option: Scatter with straight lines.

Select the orange values to make the QS plot.

EFFECT VALUES													VALUES			lb	lf	rf	rb	lb	IMAGE
Matrix	A	B	C	D	E	F	G	H	K	S	T	U	W	Y	x	-Y	-W	+W	+Y	-Y
Matrix	A	B	C	D	E	F	G	H	K	S	T	U	X	Z	y	Z	X	X	Z	Z
QS	3	3	3	8.3	8.3	8.3	40	8.3	40	40	3	3	2.03	2.03	x	-2.03	-2.03	2.03	2.03	-2.03
effect	-0.02	-0.02	-0.02	0.42	0.42	0.42	1.10	0.42	1.10	1.10	-0.02	-0.02	2.03	-2.03	y	-2.03	2.03	2.03	-2.03	-2.03
EV4	8.3	0.2	4.9	14	4.1	19	40	5.1	5.3	40	3	3	2.49	0.81	x	-0.81	-2.49	2.49	0.81	-0.81
effect	0.42	-1.2	0.19	0.65	0.11	0.78	1.10	0.21	0.22	1.10	-0.02	-0.02	2.21	-2.27	y	-2.27	2.21	2.21	-2.27	-2.27
EFFECT VALUES													VALUES			l	f	r	b	l	IMAGE
Matrix	A	B	C	D	E	F	G	H	K	S	T	U	W	Y	x	-Y	-W	+Y	+W	-Y
Matrix	A	B	C	D	E	F	G	H	K	S	T	U	X	Z	y	-Z	+X	+Z	-X	-Z
DD	3	3	3	8.3	8.3	8.3	40	8.3	40	40	3	3	0	3.10	x	-3.10	0	3.10	0	-3.10
effect	-0.02	-0.02	-0.02	0.42	0.42	0.42	1.10	0.42	1.10	1.10	-0.02	-0.02	3.10	0	y	0	3.10	0	-3.10	0

See diagrams for each matrix at Quadraphonic Systems