The election system used in the United States can be shown mathematically to be unfair.
This page shows the reasons why, and what can be done to correct the problem.
Here are the unfair parts of elections:
Voters are prevented from voting their real preferences. They can't vote against one
choice without voting for another choice. Nobody can vote against all choices and have
the vote count. Voters can't vote that they prefer both of two very similar choices. Most of
the time, voters are forced to vote against the best choice to prevent the worst choice from
winning. Here is the real reason these problems exist: There is a mathematical error in
the election process used in the United States.
The voter goes in the booth, and the machine says "VOTE FOR ONLY ONE." When
several candidates are equally desirable, the problem is: Which one to vote for? Picking a
favorite candidate makes it probable that no desirable candidate is elected. The majority
vote desiring one set of issues is split up between many candidates. A candidate with views
differing from those of the majority wins, by being the only candidate with those views. The
majority view is thwarted, by being split among candidates.
People think candidates are chosen because voters have weird ideas. Actually, there is
a BIAS in the election process. It favors candidates that are distinctly different from
the others in the race. Here is my conjecture on that bias:
CONJECTURE 1: In any Plurality Voting ("VOTE FOR ONLY ONE") election
with 3 or more candidates, probability favors the candidate most different from the
others.
Links:
CONJECTURE 2: In Plurality Voting, when two candidates with the same platform run
against one candidate with an opposing view, the platform of the two similar candidates can win
only if at least one of these is true:
- More than 2/3 of the voters favor their platform.
- The number of platform supporters choosing the same candidate is larger than the entire
opposition.
- One of the duplicate candidates drops out of the race before the election.
OTHER PROBLEMS WITH ELECTIONS:
If the voter's preference is not available on the ballot, or a candidate wins for reasons
other than a majority preference on issues, it is also not fair. Here are causes of this:
- Parties supporting the voter's preference are barred from the ballot.
- A Candidate could not meet a filing requirement, or missed a deadline.
- The law prohibits a candidate from running; he broke the law he wants abolished.
- The voter does not like any candidate running, for different reasons.
- Every candidate opposes the voter's viewpoint.
- Candidate drops out of race due to lack of funds.
- Staggered primary dates, with unfavorable states first, force candidate out of race.
- Political position lost primary election due to multiple similar candidates running.
- Slanted news coverage.
- Attempts to scare voters at the last minute.
- Secrecy about a candidate's viewpoint.
- A candidate lies to get elected, or changes views after the election.
- People change their votes to keep the worst candidate out.
- Candidate has no name recognition.
- Incumbent candidate won because other candidate was unknown.
- Incumbent won to avoid losing a powerful committee position to another state.
- The vote of the majority splits among several similar candidates.
- Different people focus on different issues, leaving no majority on any one.
- No candidate supports the majority view.
Ways to make the election system fair:
THE MAIN PROBLEM: Voters must be able to vote their real preferences without penalty.
The bias against similar platforms must be removed. For years, the method used was to
make it hard for third-party candidates to get on the ballot. This is not very fair, and
does nothing to stop the problem in primary elections. A way must be found to have
fair elections with three or more choices.
ANSWERS?
Plurality Voting ("VOTE FOR ONLY ONE") must be abolished permanently. Voters must be
able to have a say on each candidate, independently of the say they have
on the other candidates. Plurality Voting is not an independent process;
it is a disjoint (mutually exclusive) process. It is guaranteed to have interaction
problems.
Approval Voting ("VOTE FOR AS MANY AS YOU WANT") doesn't work either. It gives more
power to the voter favoring several choices, compared to the voter favoring one choice has. A way
is needed to give each voter the same power in the polls.
Ranking Voting ("PLACE THE CANDIDATES IN ORDER") doesn't work either. It can't tell
where a voter stops liking candidates and starts disliking them. A voter could unwittingly vote
for a candidate he dislikes.
CONJECTURE 3: "ONE MAN - ONE VOTE" should really mean "one man - one
vote per candidate." The voter should have the right to vote on the desirability of each
candidate INDEPENDENTLY of his vote on other candidates.
Note that, in the above voting methods, a vote for a choice has much more weight than a vote
against a choice. In some of them, you either can not vote against a choice, or you must vote
against all other choices. This difference shows the weaknesses of the above voting methods.
Unequal weightings of votes for a choice, compared to votes against a choice, cause these biases.
This fact leads to the next conjecture:
CONJECTURE 4: To be a fair election system, a vote against a choice must have
exactly the same weight a vote for the same choice has.
The biggest defect in Plurality Voting is the unequal power of votes for different choices.
This defect must be permanently eliminated in any future election system:
CONJECTURE 5: To be a fair election system, a vote for or against any choice must
have exactly the same weight that any vote for or against any other choice has. Also, a vote for
or against any political position must have exactly the same weight that any vote for or against
any other political position has.
Another problem surfaced when Ross Perot was talked into returning to the race by Bill Clinton.
It is possible in the Plurality Voting System to control the outcome of an election by having
someone run for that office with a particular platform. Thus, the need to prevent this kind of
trickery is obvious:
CONJECTURE 6: To be a fair election system, the entry or departure of a candidate
in a race must not have the power to change the outcome of the election, unless that candidate
wins the election when running.
Combining these four conjectures leads to a practical solution for this problem:
THE SOLUTION:
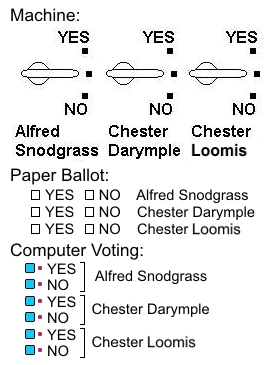 The voting device, lever, or paper ballot must have three selections for
each candidate or issue: "YES," "ABSTAIN," and "NO." If the voter
does not make a selection on that candidate or issue, the "ABSTAIN" choice is counted.
Selections on one candidate must be entirely free from interlock with selections made on another
candidate in the same race.
The voting device, lever, or paper ballot must have three selections for
each candidate or issue: "YES," "ABSTAIN," and "NO." If the voter
does not make a selection on that candidate or issue, the "ABSTAIN" choice is counted.
Selections on one candidate must be entirely free from interlock with selections made on another
candidate in the same race.
Compute the vote total for each candidate or issue by subtracting the "NO" tally
from the "YES" tally. The highest positive total wins the election. If all candidates
have negative totals, a special election with new candidates must be held. If it happens
repeatedly on an administrative office, it means the people want the office abolished.
The above forms the basis of the Independent Voting System.
The Independent Voting System ALWAYS chooses the candidate who pleases the most voters.
Links:
OTHER REFORMS:
Implement these to remove other biases:
- Let voters vote on each bill after it passes all houses and the executive.
- Make it legal for any law-abiding citizen who meets the qualifications to seek office.
- Remove petition signature requirements to be on ballot.
- Put issues as questions on the ballot too.
- Waive taxes and fees for any media giving equal free resources to all candidates.
- Prohibit campaign spending on radio, TV, newspaper, or internet advertizing.
- Have the Post Office provide two free mailings to all households in the district.
- Don't allow riders on bills, except riders that remove old law or funding to allow the
new.
- Put each budget item on the ballot as a separate question.
- Allow all eligible candidates who want to run for office to be on ballot.
- Require a candidate to file only once, on the level of government the office is on.
- Allow multiple write in votes, with YES and NO choices on each one.
- Don't require write-in candidates to register to be counted.
- Count write-ins such as "Abolish Office," and act accordingly if a write-in wins.
- The seniority system must be abolished.
- Legislative committees must be abolished.
- Slanted news coverage must be legally defined as libel.
- Abolish straight-party voting. It is meaningless in Independent Voting.
ADVANTAGES OF INDEPENDENT VOTING:
- Independent Voting ALWAYS chooses the candidate who pleases the most people.
- No primary is needed with the Independent Voting System. Since candidates do not
interfere with each other's votes, a party may have more than one candidate
running.
- Since candidates do not interfere with each other's votes, signature petitions
are no longer necessary.
- Negative campaigning by candidates will end, because voting for one candidate does not imply
voting against another candidate. Only protest groups will use negative campaigning.
- A candidate entering the race has no effect on the outcome of the election, unless
he wins the election.
- The voter can choose independently on each candidate or issue.
- Legislators should use this system too, so floor votes can be fair.
- Referendums must use this system too.
- The order of names on the ballot no longer has any influence on voters.
- A voter can vote against any number of choices.
- The voter can vote against all choices, and the vote actually counts.
- A voter can vote for two or more desirable choices.
- Voter can vote for the best choices, and against the worst choices.
- Multiple candidates do not split up the vote of a majority.
- This makes sure the voter can vote his preference on all issues.
- Candidates win on voter preferences on issues, not on preference on people.
- Free media access gives candidates the chance to be elected.
- Free broadcasts inform voters, and give the candidate enough coverage.
- Candidate gets name recognition through free media coverage.
- Public votes on issues partially nullify lies, and changes in political stand.
- People can vote to keep the worst choice out, and also vote for the best choice.
- Committees will not sway votes if they don't exist.
- The vote of the majority opinion is not split by this multiple vote system.
- Different people can focus on different issues in the votes on issues.
- If no candidate supports the majority view on major issues, the issue vote does.
- If someone really wants to vote a Plurality ballot in an Independent Voting election,
he can vote YES on one candidate, and abstain on all the others.
- If someone really wants to vote an Approval ballot in an Independent Voting election,
he can vote YES on any candidates he wants, and abstain on all the others.
DISADVANTAGES OF INDEPENDENT VOTING:
- Existing voting machines can't work with this system, unless two candidate slots are
used for each choice. This reduces the capacity of the machine.
- Each ballot cast will take more time in the booth.
- People who do not understand probability will favor the old Plurality system, because
it is simpler, even though it is wrong.
- Minorities who have benefited from the old inequitable system will oppose the change,
in order to keep their advantage.
- Statisticians who think in percentages will not like this system, because "percent
of the vote" is meaningless in Independent Voting.
- Party officials will not like the lack of a straight-party vote, because they want
to cheat, by making it easier to vote for all of their candidates. But straight-party
voting is meaningless in Independent Voting.
Three candidates, A, B, and C, run for congressman.
- Plurality Voting is used.
- Every voter decides by the candidate's stand on issue X.
- In case of a tie, a random choice is made among those tied.
- Exactly 100,000 people actually vote.
|
Three candidates, A, B, and C, run for congressman.
- Independent Voting is used.
- Every voter decides by the candidate's stand on issue X.
- A random choice is made among YES and ABSTAIN, with 90% probability of YES.
- All voters vote NO on all candidates opposing their views.
- Exactly 100,000 people actually vote.
|
| ISSUE | CANDIDATE | Voters |
|---|
| A | B | C |
|---|
| Issue X | Favors | Favors X | Opposes | 60% Favor |
|---|
| Favoring X: | 60,000 | 0 | 60,000 |
|---|
| Opposing X: | 0 | 40,000 | 40,000 |
|---|
|
| ISSUE | CANDIDATE | Voters |
|---|
| A | B | C |
|---|
| Issue X | Favors | Favors | Opposes | 60% Favor |
|---|
| Favoring X: | 60,000 | 60,000 | 0 | 60,000 |
|---|
| Opposing X: | 0 | 0 | 40,000 | 40,000 |
|---|
|
Exactly 60% of voters actually voting favor issue X, and exactly 40% oppose it. Who wins the
election?
Obviously, candidate C gets 40%, or 40,000 votes. The outcome depends on how voters
favoring issue X split up between A and B. If either A or B gets over 40% of the vote
(40,000 votes), then that candidate wins. If not, C wins.
Since a random choice is made between A and B, a binomial distribution is indicated.
The mean outcome for either candidate is the number of Voters for issue X, times the
probability that a voter for issue X votes for that candidate. That is:
|
Exactly 60% of voters actually voting favor issue X, and exactly 40%
oppose it. Who wins the election?
Obviously, candidate C gets 40,000 YES votes, and Candidates A and B get 40,000 NO
votes, from those opposing issue X. The outcome depends on how voters favoring issue X
vote on A and B. Since all 60,000 favoring issue X vote NO to opponents, candidate C
has a negative total and loses.
Since a random choice is made between YES and ABSTAIN, a binomial distribution is
indicated. The mean outcome for either candidate is the number of Voters for issue X, times
the probability that a voter for issue X votes YES for that candidate. That is:
|
| mean[A] = n[X] * Pr[A] = (60,000) * (1/2) = 30,000 votes for A |
| mean[B] = n[X] * Pr[B] = (60,000) * (1/2) = 30,000 votes for B |
|
| mean[A] = n[X] Pr[A] = (60,000) (.9) = 54,000 YES votes for A |
| mean[B] = n[X] Pr[B] = (60,000) (.9) = 54,000 YES votes for B |
|
That gives an average of 30,000 votes for each candidate favoring Issue X. The variance is
the number of voters favoring issue X, times the probability an X supporter chooses A, times the
probability an X supporter chooses B. The variance is used to get the standard deviation. The
standard deviation is the square root of the variance. We get:
|
That gives an average of 54,000 votes for each candidate. The variance is the number
of voters favoring issue X, times the probability an X supporter chooses YES, times the
probability an X supporter chooses ABSTAIN. The variance is used to get the standard
deviation (the square root of the variance). We get:
|
| Variance = n[X] * Pr[A] * Pr[B] = (60,000) * (1/2) * (1/2) = 15,000 |
| sd = SQRT(variance) = SQRT(15,000) = 122.47 votes. |
|
| Variance = n[X] Pr[YES] Pr[ABSTAIN] = (60,000) (.9) (.1) = 5,400 |
| sd = SQRT(variance) = SQRT(15,000) = 73.485 votes. |
|
Since 99% of all possible outcomes are within 3 standard deviations of the mean in a
normal or binomial distribution, the most either candidate A or candidate B can even hope
to get is:
|
Since 99% of all possible outcomes are within 3 standard deviations of the mean in a
normal or binomial distribution, the fewest YES votes either candidate A or candidate B
can expect to get is:
|
| mean[A] + 3 sd = 30,000 + (3) * (122.47) = 30,367 votes |
| mean[B] + 3 sd = 30,000 + (3) * (122.47) = 30,367 votes |
|
| mean[A] - 3 sd = 54,000 - (3) (73.485) = 53,779 votes |
| mean[B] - 3 sd = 54,000 - (3) (73.485) = 53,779 votes |
|
Neither is enough to beat C, so C wins the election when A and B are equally supported.
Issue X loses the election. This is the unfair part, because 60% of the voters favor
issue X.
|
Since 53,779 - 40,000 = 13,779, issue X wins the election. Rarely would there be an
exact tie between A and B, but with a standard deviation of only 73, a revote might be
ordered. Fortunately, there are usually minor differences between candidates that will
influence the YES vs ABSTAIN choice on each one. RESULTS:
|
| RESULTS |
| MAX | ACTUAL |
SCORE | WIN |
| A | 30,367 | 30,367 |
30,367 |
|
| B | 30,367 | 29,634 |
29,634 |
|
| C | 40,000 | 40,000 |
40,000 | WIN |
|
| RESULTS |
| YES | NO | ABST |
SCORE | WIN |
| A | 54,100 | 40,000 | 5,900 |
54,100−40,000 = +14,100 | WIN |
| B | 53,900 | 40,000 | 6,100 |
53,900−40,000 = +13,900 |
|
| C | 40,000 | 60,000 | 0 |
40,000-60,000 = -20,000 |
|
|
For issue X to win the election, at least one of these must be true:
- More than 2/3 of the voters favor issue X.
- More than 2/3 of issue X supporters favor the same candidate.
- Either candidate A or B, but not both, drops out of the race.
|
For issue X to lose the election, at least one of these must be true:
- More than 1/2 of the voters oppose issue X.
- More than 1/3 of issue X supporters don't like either A or B.
- Both candidate A and candidate B drop out of the race.
|
ACTUAL INSTANCES: Here are some actual cases where this election error has happened:
- George H. Bush is much more moderate than any other in the 1992 Republican primaries.
- Bill Clinton appears to be the only moderate in the 1992 Democrat primaries.
- Bill Clinton wins with only 43% of the vote, over the similarities of George Bush and
Ross Perot.
- Bob Dole, the moderate, wins over many conservatives in 1996 primaries.
- Compact Urban Form, the only plan that doesn't use new land, becomes Bloomington
Indiana's master land use plan, beating out 4 other plans that used new land, but in
different ways.
- Bill Clinton wins again over conservatives Bob Dole and Ross Perot.
- The example above is almost exactly what happened in the Republican primary for Indiana
US Senator in 1998. The moderate candidate won because two conservatives split the vote.
- Al Gore lost to George W. Bush when Ralph Nader took away enough votes in two states.
|
ACTUAL INSTANCES: Here are actual instances where this fair method is used:
- Congress uses it for machine votes on the floor.
- Some (but very few) surveys use it.
|
Elections would be much fairer, and would better reflect the will of the voters,
if Independent Voting became the only election system used. Follow these recommendations:
 The voting device, lever, or paper ballot must have three selections for
each candidate or issue: "YES," "ABSTAIN," and "NO." If the voter
does not make a selection on that candidate or issue, the "ABSTAIN" choice is counted.
Selections on one candidate must be entirely free from interlock with selections made on another
candidate in the same race.
The voting device, lever, or paper ballot must have three selections for
each candidate or issue: "YES," "ABSTAIN," and "NO." If the voter
does not make a selection on that candidate or issue, the "ABSTAIN" choice is counted.
Selections on one candidate must be entirely free from interlock with selections made on another
candidate in the same race.