PROBABILITY MEASURES AND DISTRIBUTIONS

The following tools are the keys to understanding probability:

DEFINITIONS:

• Experiment - An experiment is a defined set of operations that produce a probability result.
• Outcome - An outcome is any one possible result of an experiment. In set theory, this would be an element.
  Notation: o_i
• Event - An event is a set of one or more outcomes.
  Notation: E_i
• Sample Space - The sample space is the set of all possible outcomes.
  Notation: S
• Empty Event - An empty event is an event with no outcomes in it.
  Notation: {} or ∅
• Trial - A trial is one performance of the experiment.
  Notation: T_i
• Stage - A stage is one of the operations performed that make up an experiment.
  Notation: S_i
• Complement of an Event - The complement of an event is the set of all outcomes that are in the sample space, but are not the event.
  Notation: ~ E₁ or E₁'

  Let S = {o₁,o₂,o₃,o₄,o₅}     Let E₁ = {o₁,o₂,o₃}     Then E₁' = {o₄,o₅}

• Intersection of Events - The intersection of two events is the set of all outcomes that are members of both events.
  Notation: E₁ ∩ E₂

  Let E₁ = {o₁,o₃,o₅}     Let E₂ = {o₁,o₂,o₃}     Then E₁ ∩ E₂ = {o₁,o₃}

• Union of Events - The union of two events is the set of all outcomes that are members of either or both events.
  Notation: E₁ ∪ E₂

  Let E₁ = {o₁,o₃,o₅}     Let E₂ = {o₁,o₂,o₃}     Then E₁ ∪ E₂ = {o₁,o₂,o₃,o₅}

• Independent Events - Independent events do not influence each other.
• Disjoint (Mutually Exclusive) Events - Disjoint (or mutually exclusive) events have no common outcomes.
  Notation: E₁ ∩ E₂ = ∅

  Let E₁ = {o₁,o₂,o₃}     Let E₂ = {o₄,o₅}     Then E₁ ∩ E₂ = {} = ∅

• Dependent Events - Dependent events are events that change probability when other events occur. Disjoint events are dependent, because they can never occur on the same trial.
• Pairwise Disjoint Events - Multiple events where each outcome is an element of no more than one event.

  Let E₁ = {o₁,o₂}     Let E₂ = {o₄,o₅}     Let E₃ = {o₃}     Then E₁ and E₂ and E₃ are pairwise disjoint.

• Partition of the Sample Space - Pairwise disjoint events whose union forms the sample space are a partition of the sample space.

  Let S = {o₁,o₂,o₃,o₄,o₅}     Let E₁ = {o₁,o₂}     Let E₂ = {o₄,o₅}     Let E₃ = {o₃}     Then E₁ and E₂ and E₃ form a partition of sample space S.

  Properties of a Partition of the Sample Space:
  All of the events are pairwise disjoint.
  The union of all of the events equals the sample space itself.
  Each outcome in the sample space is an element of exactly one of the events.
• Types of data:

  Categorical	Numerical
  Values that cannot be measured using measuring tools The color, shape, or other discrete property of a sampled item A yes-no, multiple choice, or integer outcome of a random event   (e.g. a rolled die, playing card, genetic trait, or drawn ball)	Values that can be measured using instruments Length, volume, mass, or other measured value of sampled items Any other value that can be measured with instruments   (e.g. temperature, density, pressure, or other physical property)
  Count	Portion
  Number of occurrences of values that cannot be measured How many instances have the color, shape, or other property A non-negative integer number of outcomes of a random event   (e.g. number of heads, number with the trait, or ball count)	The portion of a given value as a fraction of that value Probabilities are portions of certainty - Fractions of wholes Restricted to these values: 0 ≤ p ≤ 1   (e.g. probability, 1/2 full, or part of any measured value)

• Replacement of Objects or Outcomes:

  Replacement	No Replacement
  Objects or outcomes are put back before the next drawing. An infinite supply of objects is available. Outcomes are part of a permanent random device.   (e.g. a flipped coin, a rolled die, or a spinner)	Objects or outcomes become unavailable or disallowed once used. Race and tournament finishing orders Objects are kept or discarded.   (e.g. a dealt hand of cards, books on a shelf, or a committee)

• The Order of Objects or Outcomes:

  Order Matters	No Order
  Outcomes are noted or arranged as they are picked. Race and tournament finishing orders. Outcomes are used for different purposes.   (e.g. president, vice president, secretary)	Objects or outcomes are chosen simultaneously. Rearranging objects does not change the outcome. Objects are dumped into a holder.   (e.g. a hand of cards, colored checkers, or a committee)

COUNTING METHODS:

Note that counts are not numerical data.

The following are methods of counting the numbers of items and outcomes in everyday life:

• The Number of an Event - The number of an event is the number of outcomes in it.
  Notation: n(E₁)

  Let E₁ = {o₁,o₃,o₅}     Then n(E₁) = 3}     Note: N(∅) = 0

• Event Addition Rule: - The following formula finds the number of the union of two events:
  Notation: n(E₁ ∪ E₂) = n(E₁) + n(E₂) − n(E₁ ∩ E₂)

  Let S = {o₁,o₂,o₃,o₄,o₅}     Let E₁ = {o₁,o₃,o₅}     Let E₂ = {o₁,o₂,o₃}     So E₁ ∩ E₂ = {o₁,o₃}
  Then n(E₁ ∪ E₂) = n(E₁) + n(E₂) − n(E₁ ∩ E₂) = 3 + 3 − 2 = 4

• Disjoint Event Addition Rule: - The following formula finds the number of the union of two disjoint events:
  Notation: n(E₁ ∪ E₂) = n(E₁) + n(E₂)     Must be disjoint!

  Let S = {o₁,o₂,o₃,o₄,o₅}     Let E₁ = {o₁,o₂,o₃}     Let E₂ = {o₄,o₅}     So E₁ ∩ E₂ = ∅
  Then n(E₁ ∪ E₂) = n(E₁) + n(E₂) = 3 + 2 = 5

• The number of the Complement of an Event - The following formula finds the number of the complement of an event:
  Notation: n(E₁') = n(S) − n(E₁)

  Let S = {o₁,o₂,o₃,o₄,o₅}     Let E₁ = {o₁,o₂,o₃}     Then n(E₁') = n(S) − n(E₁) = 5 − 3 = 2

• The Multiplication Principle - When successive stages of an experiment are independent (do not influence each other), the number of outcomes of the experiment is the product of the numbers of outcomes of each of the stages.

  Let n(S₁) = 4     Let n(S₂) = 3     Let n(S₃) = 5     Then n(S) = 4 • 3 • 5 = 60

• The Power Principle - When successive stages of an experiment are identical and do not influence each other, the number of outcomes of the experiment is the number of outcomes of one stage raised to the power of the number of stages.

  Let n(S₁) = n(S₂) = n(S₃) = 5     Then n(S) = 5³ = 125

  This works when drawn objects are replaced, and the order of the outcomes matters.

  Where there are n objects to choose from, and r choices are made with replacement, and order matters, the number of outcomes is n^r

• The Factorial Principle - The number of ways to arrange n distinct objects in a definite order without replacement is the nth factorial, written n!
  The nth factorial is the product of all of the integers from 1 to n.

  Let n = 5.     Then n! = 5! - 5 • 4 • 3 • 2 • 1 = 120

  This works when drawn objects are not replaced, the order of the outcomes matters, and all of the objects are taken.
• The Anagram Principle - The number of ways to arrange n objects composed of g groups of r_i identical objects in each group is the number of anagrams of n items of g kinds with counts of each kind r₁, r₂, ... r_g, written A(n,r₁,r₂, ... r_g).
  The sum of all of the r_i values must equal n.

  Then A(n,r1,r2,...,rg) =	n!
  	r1! r2! ... rg!

  Example: Let n = 5     Let g = 3     Let r₁ = 2     Let r₂ = 1     Let r₃ = 2    

  Then A(n,r1,r2,r3) =	n!	=	5!	= 30
  	r1! r2! r3!		2! 1! 2!

  This works when drawn objects are not replaced, the order of the objects matters, some objects are indistinguishable from others, and all of the objects are taken.

• The Permutation Principle - The number of ways to arrange r objects picked from a pool of n distinct objects, in a definite order with no replacement is the number of permutations of n items, picked r at a time, written P(n,r).

  Let n = 5     Let r = 3

  Then P(n,r) =	n!	=	5!	= 60
  	(n−r)!		(5−3)!

  This works when drawn objects are not replaced, and the order of the outcomes matters.

• The Combination Principle - The number of ways to choose a group of r objects from a pool of n distinct objects, with no order and no replacement, is the number of combinations of n items, chosen r at a time, written C(n,r).

  Let n = 5     Let r = 3

  Then C(n,r) =	n!	=	5!	= 10
  	r! (n−r)!		3! (5−3)!

  This works when drawn objects are not replaced, and the order of the outcomes does not matter.

• The Recombination Principle - The number of ways to arrange r objects reused from a pool of n distinct objects, with replacement and no order, is the number of recombinations of n items, received r at a time, written R(n,r).

  Let n = 5     Let r = 3

  Then R(n,r) =	(n+r−1)!	= C(n+r−1,r) =	5!	= 35
  	r! (n−1)!		3! (5-1)!

  This works when drawn objects are replaced, and the order of the outcomes does not matter.
  NOTE: This is rare in probability. It is included for studying unusual counting problems that do occur in daily life. Special methods (discussed later) are needed to obtain equally likely outcomes in this kind of experiment.

A note on the values used above:

• The value n-r is the number of available choices left over. The expression (n-r)! is divided out of the n! because they are the ones not chosen.
• When the value r! is in the denominator, it is divided out of the n! to remove the order of choice of r items.

Examples of each kind of experiment:

• The order matters and the objects are not replaced: permutation
  • The number of ways to win the 3 medals in an Olympic event with 5 entrants
  • Arranging 3 unlike books on a shelf from a box of 5 books
  • Taking a ball 3 times from an urn having 5 balls without replacing any balls
  • Choosing a president, vice president, and secretary from a committee of 5
• The order does not matter and the objects are not replaced: combination
  • Choosing a committee of 3 from a group of 5 students
  • Grabbing a handful of 3 balls from an urn containing 5 balls
  • Being dealt a poker hand from a standard deck
  • Choosing 3 cars from the motor pool of 5 cars
• The order matters and the objects are replaced: power principle
  • Rolling a die three times in succession
  • Taking a ball 3 times from an urn having 5 balls, replacing the ball before taking the next
  • Choosing a car for a trip 3 different times from a motor pool of 5 cars
  • Buying TV dinners for 3 meals from a store selling 5 different kinds of dinners
• The order does not matter, but the objects are replaced: recombination
  • Putting colored light bulbs in 7 sockets behind a diffuser, from 4 available colors - trading sockets has no visible effect
  • Putting 3 ads on a website from 6 available ads - the order they appear does not matter, and ads can appear more than once
  • Putting 16 color squirts from a 12 color turret into a paint can. The colors can be used more than once
  • Pushing a coin button at random 4 times on a change belt device containing a large supply of quarters, nickels, and pennies
  Note that, if equally likely outcomes are desired, special methods (described later) are needed to obtain equally likely outcomes.
• The order matters, objects are not replaced, and all objects are taken: factorial
  • The finishing order of a race with 5 cars
  • The number of ways to shuffle a 52 card deck
  • Arranging 5 unlike books on a shelf
  • Lining 25 people up in a straight line
• The order matters, the objects are not replaced, all objects are taken, there are some identical objects: anagram
  • The number of distinct "words" formed from the letters in the word "balloon"
  • The number of ways to park 4 identical red cars, 3 identical blue cars, a green car, and an orange car in a straight line
  • Arranging 3 books on a shelf from a box of 5 books, 2 of which are identical
  • The number of distinct ways to shuffle a Pinochle deck

PROBABILITY MEASURES:

The following are probability measures that occur in everyday life.

• Probability - Probability is the fraction of the trials that an event is expected to occur.
  Probability has the following properties:
  1. A probability is a fraction in the range of values from 0 to 1.
  2. If the probability of an event is 0, the event never occurs.
  3. If the probability of an event is 1, the event always occurs.
• Weight - The probability of an outcome is its weight.
  Notation: w_i = Pr(o_i)
• Odds - Odds are an obsolete measure of probability in the form S:F.
  1. S is a number, usually an integer, representing the expected number of successes in S+F trials.
  2. F is a number on the same scale representing the expected number of failures in S+F trials.
  Example: If the probability of an event is 2/3, then the odds are 2:1 (read "2 to 1") in favor of the event.
  Often an event of low probability is represented as "F:S against" (e.g. Pr(A) = 1/3 gives odds of 2:1 against A).

  It is not nearly as useful as probability.

• Sample Frequency Method - The sample frequency method consists of repeating the experiment a large number of times and recording the number of occurrences of each outcome to find their probabilities.
• Analytical Method - The analytical method consists of the use of mathematical calculations to find the probability of each outcome in an experiment.
• Probability of an Event - The probability of an event is the sum of the probability of its outcomes:

  Let E_i = {o_j,o_j+1, ... ,o_k}

  Then Pr(E_i) = w_j + w_j+1 + ... + w_k
• Equally Likely Outcomes - When all of the outcomes are equally likely, the following formulas apply:

  w_i = 1 / n(S)

  Pr(E_i) = n(E_i) / n(S)
• Sample Space Probability - Since the sample space contains all of the outcomes in the experiment, the probability of the sample space is 1.
  Notation: Pr(S) = 1
• Empty Event Probability - Since the empty event contains none of the outcomes in the experiment, the probability of the empty event is 0.
  Notation: Pr(∅) = 0
• The Value of an Outcome - The value of an outcome is how much the outcome is worth to someone performing or observing the experiment.
• Probability of the Complement of an Event - The probability of the complement of the event E is:
  Pr(E') = 1 - Pr(E)
• Event Probability Addition Rule - For any events E and F:
  Pr(E ∪ F) = Pr(E) + Pr(F) - Pr(E ∩ F)

  Note that, since E ∩ F occurs twice, once in E, and also once in F, one of them must be subtracted out.

• Mutually Exclusive Event Probability Addition Rule - For any disjoint events E and F:
  Pr(E ∪ F) = Pr(E) + Pr(F)

  Note that, since E ∩ F is empty in disjoint events, its probability is 0, and it does not have to be subtracted out.

• Independent Event Probability Multiplication Rule - When events are independent:
  Pr(E ∩ F) = Pr(E) • Pr(F)
• Conditional Probability - The conditional probability of the event A, given that event B is known to have occurred, is Pr(A|B)
  Pr(A|B) = Pr(A ∩ B) / Pr(B)

  The probability of the event A, given that B has occurred, is the probability that both events occurred, divided by the probability that event B occurred.

• Stochastic Process - An experiment that is made up of multiple stages is called a stochastic process.
• The Parts of a Probability Tree:
  • Root - The starting point of the tree is the root.
  • Node - Any stopping point on a tree is a node, represented by a circle.
  • State - The node at the current point in the performance experiment is the state.
  • Branch - A portion of a tree connecting two nodes is a branch, represented by a line.
  • Branch Probability - A branch probability is the conditional probability of following a particular branch, represented by a weight placed by the line representing the branch.
  • Leaf - A leaf is an ending node, representing a final outcome of an experiment. The experiment ends when it reaches a leaf.
  • Leaf Probability - The leaf probability of a leaf is the probability of reaching that leaf.
  • Stage - A stage is any of the several sequential acts that make up the experiment.
  • Stage Outcome - The result of performing a stage is the stage outcome.
  • Transition - A transition is the performance of a stage, resulting in a stage outcome, and changing the state of the experiment.
• The number of Outcomes on a Tree - The number of outcomes on a tree is found by counting the leaf nodes.
• Use of the tree to represent an experiment:
  • Place the root at the left, and add each stage to the right of the previous stage.
  • Use a branching of lines to represent each stage in the experiment. Place a branch probability (if known) on each branch.
  • Use a column of nodes (circles) to represent the possible outcomes of that stage.
  • Leave enough space for the entire tree. It can become rather tall.
  • 
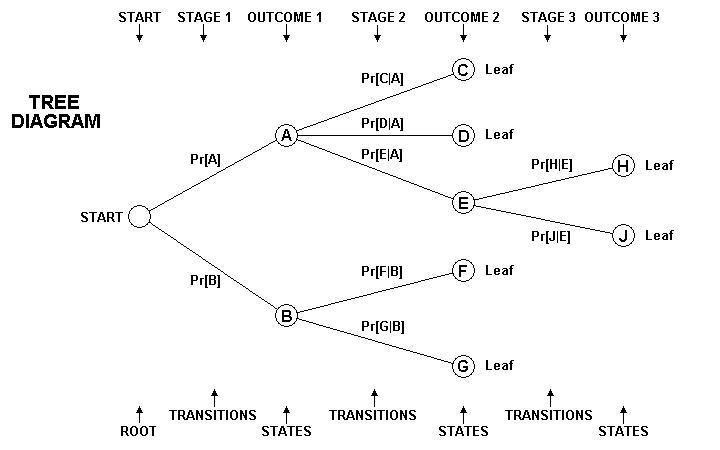
  • A sample experiment:
    1. Urn A contains cards C, D, and E.
    2. Urn B contains cards F and G.
    3. Card E has an H printed on one side and a J on the other side.
    4. Stage 1: Select either urn A or urn B.
    5. Stage 2: Draw a card from the selected urn.
    6. Stage 3: If card E is drawn, flip the card in the air and note which side comes up.
• The Probability of a Particular Leaf - The probability of reaching a particular leaf is found by multiplying the branch probabilities found on all of the branches leading from the root to the leaf.
• The Probability of an Event containing Multiple Leaves - The probability of an event containing multiple leaves is found by finding the probabilities of the leaves in the desired event, and then adding the probabilities so found. Since they are single outcomes, they are always pairwise disjoint, so they can be added.
• Bayes Probability - Bayes probability is a method of finding Pr(B|A) in a system where it is easy to find various forms of Pr(A|B).
  Use the following procedure:
  1. The sample space is partitioned into n subsets S₁ through S_n.

  2. Pr(S1|A) =	Pr(A|S1) Pr(S1)
     	Pr(A|S1) Pr(S1) + Pr(A|S2) Pr(S2) + ... + Pr(A|Sn) Pr(Sn)

  This is easiest to do with a tree.
  1. Multiply out the leaf probabilities of all of the outcomes where event A happens.
     These are Pr(A|S_i) Pr(S_i) values.
  2. Find the sum of the probabilities just found.
  3. Find the leaf with the desired event S1.
  4. Divide the desired leaf probability Pr(A|S₁) Pr(S₁) by the sum calculated above.

REPETITION PROBABILITY:

Note that the following distributions use categorical data:

• Bernoulli Process - A Bernoulli process is a repetition of the same operation a specified number of times.
  It has the following properties:

  Explanation of the various parts: If the process were placed on a tree, C(n,r) counts the number of tree leaves with r successes. p is the probability of success r is the number of successes 1-p is the probability of failure. n-r is the number of failures.

  • The process has replacement
  • The order is unimportant in this type of measure.
  • The probability of success p is always the same for all of the operations.
  • The operation is repeated n times.
  • The probability of r success in n trials is:
    Pr(r successes) = C(n,r) p^r (1-p)^n-r.

    Example:
    Let n = 5
    Let r = 3
    Let p = 1/4
    Then Pr(3 successes) = C(5,3) 1/4³ (3/4)² = 10 (1/64) (9/16) = 90 / 1024 = 45 / 512

  • The Binomial Distribution uses the Bernoulli probabilities for all of the possible values of r in a random variable.
  • The Bernoulli Process and the Binomial Distribution are used when replacement occurs.

• The Partitioning Process - The partitioning process is used to find probabilities where several kinds of objects can be selected, but where replacement does not occur.
  It has the following properties:

  Explanation of the various parts: j is the number of objects in the pool. k is the number of pool objects called successes. (j-k is the number counted as failures.) n is the number of objects drawn. r is the number of successes drawn. (n-r is the number of failures drawn.) C(k,r) is the ways to draw r successes from k success objects. C(j-k,n-r) is the ways to draw n-r failures from j-k failure objects. C(j,n) is the ways to do the experiment, drawing n from a pool of j objects.

  • The process does not have replacement.
  • The order is unimportant in this type of measure.
  • The probability of success for the operation changes as objects are removed.
  • There are j objects in the pool to be chosen.
  • k of those objects are defined as successes.
  • The objects are drawn simultaneously.
  • The probability of r success out of n is:

    Pr(r successes) =	C(k,r) C(j-k,n-r)
    	C(j,n)

    Example:
    Let j = 5 in the pool
    Let k = 3 are successes
    Let n = 4 drawn
    Let r = 2 successes drawn

    Then Pr(2 successes) =	C(3,2) C(2,2)	=	3 • 1	=	3
    	C(5,4)		5		5

  • The Hypergeometric Distribution uses the Partitioning probabilities for all of the possible values of r in a random variable.
  • Some books use this, but do not identify it by name.
  • The Partitioning Process and the Hypergeometric Distribution are used when replacement does not occur.

  The Partitioning Process can also be used with multiple kinds of identical objects, but it is no longer a distribution.
  It has the following properties:

  Explanation of the various parts: j is the number of objects in the pool. ki is the number of objects of kind i in the pool. g is the number of kinds of objects in the pool. n is the number of objects drawn. ri is the number of objects of kind i drawn. C(ki,ri) is the ways to draw ri out of ki objects of kind i. C(j,n) is the ways to do the experiment, drawing n from a pool of j objects.

  • The process does not have replacement.
  • The order does not matter.
  • The probabilities of each of the kinds of objects changes as objects are removed.
  • There are j objects in the pool to be chosen, divided into g kinds, with various numbers of each kind: k₁,k₂, ... ,k_g.
  • From the pool of j objects, n are drawn.
  • Different numbers r_i of each of the g kinds are drawn, up to the number available of each kind k_i: r₁,r₂, ... ,r_g.
  • The sum of the numbers drawn r_i is n
  • The objects are drawn simultaneously.
  • The probability of each outcome is:

    Pr(or1,r2,...,rg) =	C(k1,r1)•C(k2,r2)• ... •C(kg,rg)
    	C(j,n)

    Example:
    Let j = 5 in the pool
    Let g = 3 kinds
    Let k₁ = 2 of kind 1
    Let k₂ = 1 of kind 2
    Let k₃ = 2 of kind 3
    Let n = 4 drawn
    Let r₁ = 2 of kind 1 drawn
    Let r₂ = 1 of kind 2 drawn
    Let r₃ = 1 of kind 3 drawn

    Pr(2,1,1) =	C(2,2)•C(1,1)•C(2,1)	=	1 • 1 • 2	=	2
    	C(5,4)		5		5

  • The Partitioning Process for multiple types is used when replacement does not occur.

RANDOM VARIABLE:

• Random Variable - A random variable is an experiment where the outcomes in the sample space are identified by real numbers, called values.

  Note that, although real numbers are used, the outcomes are still categorical data because only certain values can occur.

• Binomial Random Variable - A binomial random variable uses as values the numbers of successes in a Bernoulli process.

  The binomial random variable is used where replacement occurs.

• Binomial Distribution - A binomial distribution is a binomial random variable.
• Hypergeometric Random Variable - A hypergeometric random variable uses as values the numbers of successes in a partitioning process.

  The hypergeometric random variable is used where replacement does not occur.

  Some books use this, but do not identify it by name.

• Hypergeometric Distribution - A hypergeometric distribution is a hypergeometric random variable.
• Normal Distribution - The normal distribution is a variation of the binomial distribution where any numerical value can be used, not just integer values. The normal distribution works for numerical or categorical data, but is designed for numerical data.
• Student's T Distribution - The T distribution is a variation of the hypergeometric distribution where any numerical value can be used, not just integer values. This works with numerical data.
• Other distributions:
  • Chi Squared Distribution - The chi squared distribution is used to test goodness of fit of a theoretical distribution to actual data.
    It is used with a crosstable to compare outcomes that are counts of categorical data.
  • Exponential distribution - An exponential distribution is the distribution of times between events for independent events with an average repetition rate.
  • F Distribution - The F distribution is a distribution of variations in standard deviation.
  • Geometric Distribution - The geometric distribution is a distribution of the number of failures in a binomial event before the first success occurs.
  • Negative Binomial Distribution - The negative binomial distribution is a distribution of the number of failures in a binomial event before a given number of successes occurs.
  • Poisson Distribution - The Poisson distribution is distribution of the number of occurrences in a given time of an independent event with an average repetition rate.
• Probability Density Function of a Random Variable - A probability density function assigns a weight (probability) to each value of the random variable. The weights assigned must add to 1.

  Example: A dice game at a carnival costs $3 per play. If you win, you get $4, if you lose, you get nothing. A win is a roll of 2, 3, 4, or 5.
  Here is a chart of the random variable of this game:

  Die roll	Value	Weight
  1	-$3	1/6
  2	+$1	1/6
  3	+$1	1/6
  4	+$1	1/6
  5	+$1	1/6
  6	-$3	1/6

EXPECTED VALUE:

• Expected Value - The expected value E(x) is the average value to be expected from many repetitions of the experiment.
• Mean Value - The mean value μ is the expected value. μ = E(x)
• Standard Deviation - The standard deviation of a random variable is the expected amount of deviation from the mean.
  • The population standard deviation σ of a random variable is the expected deviation from the population mean value μ.
  • The sample standard deviation s of a random variable is the expected deviation from the sample mean value x̄.
  • Use the population standard deviation when the entire studied group is included.
  • Use the sample standard deviation when a sample was taken.
• Variance - The variance is the square of the standard deviation.
  • The population variance σ² is the square of the standard deviation σ.
  • The sample variance s² is the square of the standard deviation s.
• Random Variable Expected Value - The expected value of a random variable is the sum of the products of the value of each outcome and its weight.

  Example, taken from the random variable example above:

  Die roll	Value	Weight	Product
  1	-$3	1/6	-$3/6
  2	+$1	1/6	+$1/6
  3	+$1	1/6	+$1/6
  4	+$1	1/6	+$1/6
  5	+$1	1/6	+$1/6
  6	-$3	1/6	-$3/6
  Total		1	-$2/6

  The expected value is -$2/6 (reduces to $1/3), or a loss of 33 1/3 cents per play on the average, even though the actual loss is never this amount.
• Random Variable Variance - The variance of a random variable is measure of its variation. Compute it using the procedure below:
  1. Find the deviation of each value x from the expected value μ by subtracting the mean μ from it.
  2. Square each deviation.
  3. Multiply each squared deviation by its weight.
  4. Sum the resulting products.
  Example, taken from the expected value above:

  Die roll	Value	Weight	Product	Deviation	Squared Dev	Product
  1	-$3	1/6	-$3/6	-16/6	64/9	32/27
  2	+$1	1/6	+$1/6	+8/6	16/9	8/27
  3	+$1	1/6	+$1/6	+8/6	16/9	8/27
  4	+$1	1/6	+$1/6	+8/6	16/9	8/27
  5	+$1	1/6	+$1/6	+8/6	16/9	8/27
  6	-$3	1/6	-$3/6	-16/6	64/9	32/27
  Total		1	-$2/6			96/27

  The variance is 96/27 = 32/9

  Note that the fractions obtained in the process were reduced, but just enough to obtain a common denominator.

• Random Variable Standard Deviation - The standard deviation of a random variable is the square root of the variance.

  In the example above, the standard deviation is √(32/9) = 4/3 √2 , or approximately $1.89.

• Binomial Expected Value - The expected value of a binomial random variable is: E(x) = np.

  Multiply the number of trials by the probability of success.

• Binomial Variance - The variance of a binomial random variable is:

  Var(x) = n p (1-p)

• Binomial Standard Deviation - The standard deviation of a binomial random variable is the square root of its variance:

  σ = √(n p (1-p))

• Hypergeometric Expected Value - The expected value of a hypergeometric random variable is the number of success objects in the pool times the number of drawings, then divided by the pool size.

  E(x) = k n / j

• Hypergeometric Variance - The variance of a hypergeometric random variable is the number of drawings, times the number of success objects in the pool, times the number of failure objects in the pool, divided by the square of the pool size.

  Var{x} = n k (i-k) / j²

• Hypergeometric Standard Deviation - The standard deviation of a hypergeometric random variable is the square root of the variance:

  σ = √(n k (i-k) / j²)

• Using the Normal Distribution to Approximate the Binomial Distribution - The following must be true to use the normal approximation of the binomial distribution:
  • n is the number of trials
  • p is the probability of success
  • j is the lower limit of the number of successes wanted
  • k is the upper limit of the number of successes wanted
  • n p > 5
  • n (1-p) > 5
  • 0 < j < k < n
  To find the probability that X is between values j and k:
  1. Find the mean μ = n p
  2. Find the standard deviation σ = √(n p (1-p))
  3. Use as the lower normal limit: j-0.5
  4. Use as the upper normal limit: k+0.5
  5. Find the approximation of Pr(j-0.5 < X < k+0.5) by finding the probability Pr((j-0.5-μ)/σ < Z < (k+0.5-μ)/σ)

     Note that the above is simply applying the normalizing equation Z = (X-μ)/σ by substituting the variables j and k for X.

Links:

• Finite Mathematics
• Big number calculator for counting outcomes
• What is a random number?
• Computers, Science, and Measurement