DISCOVERIES IN MODERN PHYSICS
NEW OBSERVATIONS USING TRIGONOMETRIC RELATIVITY
The application of trigonometry to the Relativity equations led the page author to some startling conclusions:
While reviewing the Lorentz equations on the Relativity effects on length, mass, time, and motion, the page author noticed that they have trigonometric equivalents. Those then revealed more information, plus a visual model that doesn't use speeding trains.
EINSTEIN'S POSTULATESEinstein's Postulates are:
|
THE LORENTZ EQUATIONS ARE EQUATIONS, NOT INEQUALITIESWhere the following are true:
The Lorentz transformation equations are: Standard Form:
Substituting a value δ for the square root portion of the above equations: Delta form:
Notice that these are equations, not inequalities. Yet, most calculations are done as though they were inequalities. |
THE EQUATIONS ARE THE EQUATIONS OF A TRIANGLE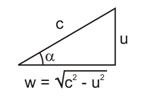
Some algebra on the delta equation:
The hypotenuse of the Relativity triangle is always c, and will be referred to as the c-vector. The side of the Relativity triangle opposite the angle α is always u, the relative velocity between the reference frames. Defining w, the projection of the observed c-vector onto the observer's c-vector, and relating w, u, and c
|
SOLVING THE TRIANGLE PROVIDES ALL OF THE EQUATIONS FOR RELATIVITY EFFECTS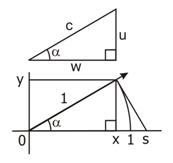
Substituting partial trigonometric values for δ gives partial Trigonometric Relativity equations: Trigonometric Relativity - partial form:
Note that R (clock rate) and f (frequency) are the same thing. Substituting complete trigonometric values for δ gives the final Trigonometric Relativity equations: Trigonometric Relativity - final form Finding Observer's Observed Values:
Finding Actual Values in Original Frame:
Finding Relative Velocity Between Frames:
Postulate 1: All effects of Relativity are actually vector component projections. Note that the postulate numbers are from the forthcoming book mentioned below. These projections are all made between the hypotenuse of the triangle and one of the other sides. The projection of elapsed time appears different, because time is normally an inverse value. |
FAST CALCULATION OF RELATIVITY WITH TRIGONOMETRY ON A CALCULATORUsing a scientific calculator to find relativistic values the easy way: (To find the secant, find the cosine, and then use the 1/x reciprocal button.) (To find the arcsecant, use the 1/x reciprocal button, and then find the arccosine.) Finding Observer's Observed Values with a calculator:
Trigonometric Relativity - Finding Actual Values in Original Frame:
Trigonometric Relativity - Finding Relative Velocity Between Frames u:
|
EVERYTHING MOVES AT THE SPEED OF LIGHT
In the equations for length, mass, time, and motion at relativistic speeds, there are equal signs, not less-or-equal signs. When all of these equations are applied simultaneously, they show that everything moves at the speed of light in one way or another. Note that the speed of light is the vector sum of the motion through space u and the motion through time w, as seen by the observer. So how do we see objects moving at speeds slower than light? They are moving relative to each other at speeds slower than light. Their lightspeed motion vectors produce a resultant relative speed that is slower than the speed of light. All components are moving at the speed of light, but in different directions. Postulate 2: Everything always moves at the speed of light. Different frames of reference just move at different vector angles in space-time. The total of all motions of any object (and of any particle of the object) always sum to the speed of light. This includes motion in space, motion in time, internal motions, and the spinning and vibrations of any subatomic particles. |
TIME IS THE MOTION AT THE SPEED OF LIGHTWe do not notice the motion at the speed of light as a motion through space. We notice this motion as the flow of time instead. The direction of the lightspeed motion (called the lightspeed motion vector) becomes the time dimension for the observer within that frame of reference. Motion though the dimension the observer is moving through at lightspeed is normally measured in intervals of time, rather than in distances through space. But this distance can be calculated for the case of the motion of empty space through time. Multiply the speed of light by the elapsed time to get the distance though the time dimension that this space traveled. Postulate 3: Time is the motion of the frame of reference through its own time dimension at the speed of light. Each frame of reference has its own time dimension The Relativity Invariant: vx2 +vy2 +vz2 +w2 = c2 The sum of all instantaneous motion vectors on a particle is always the speed of light c. |
THE TIME DIMENSION IS LORENTZ-CONTRACTED TO ZERO LENGTHBecause the space the observer is in is moving at the speed of light in the direction of the time dimension, the time dimension is Lorentz-contracted to zero length, as seen by the observer. Thus, we do not see it as a physical dimension. Postulate 4: The Lorentz contraction of space to zero length in the direction of the c-vector motion causes the observed effects of Relativity. But note that the time dimension is in a different direction for observers moving in different directions through spacetime. We see part of the other observer's time dimension, and the other observer sees part of our time dimension. The various Relativity effects are caused by the different c-vector angles of the observers, and the correspondingly different directions of each observer's time dimension. Of the 4 dimensions, we see only three of them as a result. This is the reason that the trigonometric functions, rather than the hyperbolic functions used by others, are used here. The use of the hyperbolic functions is based on allowing speeds slower than the speed of light. |
ACCELERATION CHANGES THE C-VECTOR ANGLE, NOT THE SPEED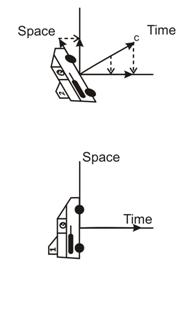
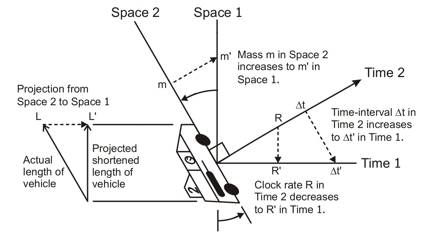
As a force is applied to an object to change its velocity, its actual speed does not change. This speed, in the direction of the lightspeed motion vector (c-vector) for the object (the direction of the flow of time), is fixed by the mass effects of that object. What does change is the direction of the object's c-vector motion through spacetime. Postulate 6: Each mechanical force really acts as a torque to rotate the direction of the c-vector of the object the force acts on. As a car speeds up on the freeway, it changes its lightspeed motion vector angle, so it is at a slight angle to the lightspeed motion vector angle of the road. Thus, the car appears to be moving at a speed less than the speed of light, relative to the road. That's why you can be arrested for exceeding 65 mph, even though the road, the car, and the police car are all moving at speeds near lightspeed. In the diagram at the right, the vertical direction is space, but the horizontal direction, to the observer in the Relativity ship numbered 1, is time. Relativity ship number 2 is relatively moving away from ship 1 at a large fraction of the speed of light. This rotates its c-vector (labeled c in the drawing) in the direction of the relative motion. Note that the c-vector of ship 1 points straight to the right. This causes the observer in ship 1 to see a foreshortening of the length of ship 2 because its length is partially rotated into observer 1's time dimension. He sees the foreshortened length of the ship along his space dimension along the direction of relative motion. |
RELATIVITY WORKS BOTH WAYS
Each observer sees Relativity effects in the other observer's ship, but not in his own. This is because each ship's c-vector is rotated relative to the other ship's c-vector. In this case, the ships are moving apart at high speed. Each observer sees the following effects in the other observer's ship:
But each observer sees these abnormal effects occur on the other ship, but not on his own ship. And the same effects are observed whether the ships are moving apart or approaching each other. One difference between approaching and receding is the difference in observed frequencies. The Doppler effect raises the frequency of signals emitted by an approaching object, but lowers the frequency from a receding object. But the Relativity effect reduces the frequency of emissions from either an approaching object or a receding object. The observation is a combination of the two. |
HOW EACH OBSERVER SEES THE OTHER SHIP'S CLOCK RUNNING SLOWER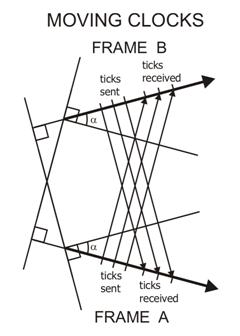
Each observer sees the clocks on the other ship running slower, whether the ships are moving toward each other or away from each other. The diagram shows why: The c-vectors (and the orientations of the time dimensions) are at different angles, thus the received ticks of the clock are farther apart. Note that this effect occurs in addition to any Doppler effect caused by the changing distance between the ships. Again, the Doppler effect raises the frequency of signals emitted by an approaching object, but lowers the frequency from a receding object. But the Relativity effect reduces the frequency of emissions from both approaching and receding objects. Note that the light emitted by any object must stay within the space dimensions it was emitted in. When it enters a frame of reference using different space and time dimensions, the slowing down of the clock pulses occurs. The Twin Paradox: Another question comes up: If the principle of Relativity is correct and valid for all natural events (an Einstein Postulate), then it would seem that the aging of one twin, but not the other, could not happen. But the key point is acceleration. The twin making the trip changes velocity 4 times:
Thus, the twin changed frames of reference four times. He experiences only a few years, while the stay at home twin ages several decades. A satellite or space station in orbit is constantly changing frames of reference, because it is following a curved path. Thus, it also has its time slowed down. |
INTERNAL MOTIONS SLOW MATTER DOWNBecause matter has rotating and vibrating components that are part of the characteristics of matter, nothing made of matter can achieve the speed of light in the linear direction of the motion through time. The lightspeed vectors are curved into helixes and sinewaves by the rotations and vibrations of the particle components of the matter. Postulate 5: Due to internal spins and motions, matter can never fully attain the speed of light in either space or time. This means that matter slows down a little in the linear direction of the lightspeed vector of the space around it. It moves slower than empty space would otherwise move along its time axis. Although the individual infinitesimal parts of a particle are all moving at exactly the speed of light through spacetime, the collective object made of this moving matter is moving slower in a linear direction. The rest of the motion at the speed of light is used up in the rotation and vibration of the parts that make up the object. |
SLOWER MOVING MATTER BENDS SPACE BACKWARDBecause the collective matter in a real object is moving forward in the time dimension at a slower speed than lightspeed, the matter bends space backward in the time dimension. Space then acts like a giant rubber sheet, stretching to pull the slower matter along behind it. This curves the space around the matter, slowing down and bending the light passing through that space. The limit on the speeds of all of the parts of matter could also explain quantum mechanics, as well as radioactivity and particle decay probabilities. Something might be forced to choose between moving at a speed other than lightspeed, and falling apart while maintaining lightspeed for all of the resulting parts. Lightspeed always wins. |
THE BACKWARD BENDING OF SPACE CAUSES GRAVITY
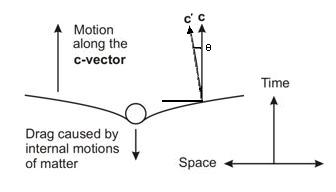
The rubber sheet theory of gravity is real! As the space bends backward in time around a massive object, the space is sloped on each side of that object. The presence of other objects also pulling backward on the motion of space through time causes the space around one object to be sloped toward the other object. Thus, the two objects will tend to move toward each other. This bending of space causes gravity! Postulate 7: Due to internal spins and motions, the proximity of matter slows the motion of space through the time dimension, causing gravity. The bending of space to cause gravity also shows why antigravity is impossible. To counteract the bending of space backward in the time dimension, an object would either have to have its individual particle components traveling faster than light, or it would have to stop all of the rotating and vibrating motions of its particle components. In either case, the matter would stop being matter. The effect of gravity as acting on space being like a huge rubber sheet has been used as an example, but until now, there was no explanation of what pulls the rubber sheet "downward" when mass is present. The "sheet" of the universe is pulled backwards by matter to avoid any speed other than the speed of light. Notice how the bending of space changes the angle of the c-vector, rotating it toward the mass through the angle θ. This bending causes the gravitational attraction between the mass and any mass at any such point p. The formula for the bending of space will be found in the book mentioned below. This bending of space also causes the path of light to bend (one of Einstein's predictions). Black holes are a special case. They slow down space so much that the hole locally stops the expansion of the universe. The matter inside the black hole orbits the center of the hole at the speed of light without moving forward in normal time. As more matter enters the black hole, it orbits at the point in time when it entered the hole. Gravity is due to a bending of space in the space-time continuum. The curvature of space causes the c-vector motion of any mass to change its direction toward another mass. Postulate 8: There is no such thing as a field. What appears to us to be a field is actually a distortion of space-time that becomes necessary to prevent a violation of Postulate 2. The possibility here is that all fields (electric, magnetic, etc.) are actually distortions of space necessary to prevent any particle from moving at a speed other than the speed of light. An atom could be likened to a circus performer balancing many spinning plates on sticks, except that it hardly ever drops a plate. However, if it reaches a state where it can't keep all of the particles in it moving at exactly the speed of light, either a particle or energy must be ejected from the atom, causing a radioactive decay. |
THE UNIVERSE IS AN EXPANDING 4-D SPHEREThe Big Bang should really be referred to as the Big Flash, because it should be totally energy in the beginning. At the time of the Big Flash, the universe was very small. Space became the expanding surface of a 4-dimensional sphere surrounding the original point of the Big Flash. All points in today's space are nearly equidistant from the original point of the Big Flash. They surround it within the surface of the 4-D sphere. Space directions are directions around the surface of the 4-D sphere, while the lightspeed motion through time is usually oriented in a direction away from the center of expansion, moving along a radius going back to the center of this 4-D sphere. Light follows an equiangular spiral from its source to the point of observation, following the curve of expanding space. Postulate 9: Time, motion, the speed of light, Relativity, and gravity are all different manifestations of the same thing. |
THE UNIVERSE ITSELF EXPANDS AT THE SPEED OF LIGHTThe space in the universe is moving outward along any radius at the speed of light. Thus, the circumference is expanding along any great circle at 2 times π times the speed of light. This means that we can't see any part of the universe that is moving away from us relatively at a speed greater than lightspeed. Note that the relative speed of two objects can be any speed. But the relative speeds of objects in the same part of space cannot exceed lightspeed. Only the expansion of space itself can make objects move away from each other at speeds greater than lightspeed. Those objects must be farther apart than the radius of the 4-D sphere. Note that this speed of expansion is necessary to make gravity work. Without it, there is no gravity. |
THERE IS NO INFLATIONARY PERIODThis model of the universe needs no inflationary period to make the area of the emission of the 3-kelvin background radiation be very large. As the universe expanded, the light followed the curvature of the expanding 4-D sphere of space. As the curvature changed the angle of the light, it also redshifted it. Thus, the part of the universe that emitted this background radiation was very small when the radiation was originally emitted. The radiation followed the curvature of space as the space expanded. As the curvature followed increases, the redshift becomes more pronounced, finally reaching the 3 kelvin blackbody radiation. This also explains the extreme uniformity of the background radiation as it is seen in all directions. The radiating area WAS very small at the time the radiation was released. So there is no mystery about why the background radiation is so uniform. There is no center to the current universe in space. It is a 3-dimensional surface of a 4-dimensional sphere. Like the 2-D surface of an ordinary 3-D sphere, there is no center. The center is in the interior of the ordinary sphere, and likewise, the center of the 4-D sphere is equidistant from any point on the 3-D surface. This center of the 4-D sphere is back in time, at the point of the big flash. |
THE OBSERVED INCREASE IN THE SPEED OF EXPANSION IS A RELATIVITY EFFECTBecause the universe is an expanding 4-D sphere, the various observed expansion speeds are actually cosine observation effects. The speeds of distant objects are being observed at angles, because they are partway around the curvature of space on the 4-D sphere. The objects are actually moving close to the speed of light, but we see a speed resulting from the angle between the object's lightspeed velocity vector and the observer's lightspeed velocity vector. The farther away the object is, the larger the angle between the vectors. The distance to the object seems greater too, because the light followed the curve of the shell of space to get here. Thus, space is not really expanding at an increasing rate. Instead, the observation that it expanded slower at an earlier time is another effect of Relativity. |
THE 4-D SPHERE EXPLAINS DARK MATTER AND ENERGYThe universe has more matter in it than we can see. The dark matter is in the portion of the universe that is moving away faster than lightspeed. It is on the other side of the 4-D sphere. But since most of that matter is also located in a direct line that is in a direction backward in time, through the center of expansion and out the other side, it might have detectable effects. Dark energy is likewise found in the invisible parts of the universe on the other side of the 4-D sphere. But it is not needed to explain the speed of the expansion of the universe. There is no need of another explanation for the expansion of the universe if everything moves at lightspeed. On the contrary, an explanation would be needed if the universe were not expanding. |
GRAVITY CAN'T SLOW THE UNIVERSE EXPANSIONBecause the expansion of the universe causes gravity, gravity will never brake the expansion. But the expansion of the universe does not expand the space inside matter. We will always be able to see the same objects in space, because space is always expanding at the same speed. They will just appear to be farther apart. The speed of the expansion of the universe depends on only the speed of light. Nothing else, including the amount of matter in the universe has anything to do with the speed of expansion. The speed of light forces the speed of expansion to be a specific value. The experiment to determine the curvature of the universe failed to produce the correct result because it assumed that gravity would slow the expansion. But since the expansion speed is permanently the speed of light, and since the expansion causes gravity, gravity can't slow the expansion. If gravity somehow slowed the expansion, gravity itself would cease to exist. |
A ROCKET AND A BULLET HAVE DIFFERENT RELATIVITY EFFECTSBecause the power source is in a different frame of reference, a bullet will take more energy than a rocket will to reach the same speed. All of the energy needed to accelerate a bullet to a very high velocity must come from the power source in the other frame of reference. This is the effect where an atom smasher has to exert more and more force to make the particle move faster as the speed increases. The particle sees a weaker and weaker force being applied to it as it speeds up, because the force is exerted at an angle to the velocity vector. The rocket should not have this trouble, because its frame of reference is changing as it applies the force to speed up. The rocket is carrying its power source. The person on board the rocket will also not see it taking abnormally more power to go faster. But the person in the frame of reference the rocket left behind will see an increase in power and mass, and a decrease in acceleration, due to the Relativity effects that the pilot does not see. So, while the observed effects appear to be the same, the actual energy used up (in the form of fuel expended) is very different in each case. |
A WORMHOLE IS NOT A SHORTCUTSome physicists have postulated that a wormhole could be used to travel quickly from one part of the universe to another. But with the speed of expansion and the size of the universe shown by this theory, it would take longer to get there through the wormhole than it would take following normal space. Black holes use up their entire lightspeed motion vectors rotating the matter components inside them, so they do not move forward in normal time. Possibilities of time travel do appear in this model, but enormous amounts of energy would be needed to accomplish it. We know forward travel is possible. But we do not know what would happen if someone somehow aimed a lightspeed motion vector in the opposite direction to the normal flow of time. |
THE UNIVERSE LOOKS INSIDE OUT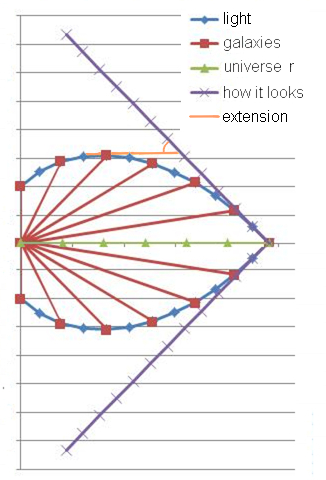
Since the universe is an expanding 4-D sphere, light must follow the 3-D surface of that sphere, which we see as the observable universe. The combination of the expansion and the motion of light makes the light follow a spiral path from the point it was emitted to the point where it is seen or photographed:
|
STUFF WOULDN'T WORK IF THE EXPANSION WERE SLOWERThis theory of Relativity is unique in that it actually explains why gravity and other effects happen. But there is one important implication to this theory: The expansion of the universe must be at or very close to the speed of light. If it is not, the theory predicts some very odd effects. The following things would not work if the universe were expanding slower than very close to the speed of light.
|