CALCULATING SIGNAL PROGRESSION

THE PRINCIPLE

The method is based on finding the solution to a linear equation with the following properties:

• The slope of the line is based on the distance involved, the speeds involved, and the cycle length of the signals.
• The y-intercept is based on the position of the first signal in the plan.
• Each signal should be as close as possible to a multiple of half the cycle length in travel time from the x-intercept.
• An error value is calculated for each signal. It is the signed distance (in half cycles) between the signal's location on the line and the nearest half cycle.
• A value that is half the absolute value of the error value is calculated to decide how to phase the signal.

THE PROCESS

Here is the method used in the progression web page on this site:

EXPLANATION OF THE PROCESS

1. The conversion factor (Convert)

   The conversion factor is used to compensate for the use of different units of measure for speed and distance:

   • If meters per second and meters are used the conversion factor is 1.
   • If kilometers per hour and meters are used, the conversion factor is 1000/3600.
   • If feet per second and feet are used, the conversion factor is 1.
   • If miles per hour and feet are used, the conversion factor is 5280/3600.

   One of these four systems must be chosen for the calculations.

2. Cycle Length (CycLen)

   For progression to occur, all of the progressed signals must be related by a common cycle length. This is the number of seconds from the end of the green on the progressed street for one cycle to the end of the green on the progressed street for the next cycle.

   This is the reason the light stays green on the progressed street when no traffic is using the green at the moment. The signal must stay in synchronization with the other signals. Actuated signals can vary the amount of the other phases, but the end of the green for the progressed street must always be synchronized to the timing plan.

3. Master Offset (MasOffset)

   The master offset, in units of whole cycle lengths, adjusts the position of the timing plan, so the first signal does not have to be at a perfect half cycle position. All of the signals are adjusted by this amount.

4. Block Length (BlkLen)

   The block length is the distance (in the chosen unit of measure for distance) from one signal to the next. The first signal has a block length of zero. The second signal has the block length from the first signal to the second signal, etc.

5. Speed (Speed)

   The speed is the actual progression speed (in the chosen unit of measure for speed) in the block given. The second signal gets the actual speed over the section between the first signal and the second signal, etc. The first signal gets the same speed the second signal gets.

6. Split (Split)

   The split is the fraction of the cycle given to the progressed street. It must be between 0 and 1.

7. Cumulative Distance (CuDist)

   Cumulative Distance is the distance from the first signal to this signal.

8. Adjusted Speed (AdjSpd)

   This is the speed, but converted to feet/second or meters per second.

9. Travel Time (TravTim)

   Travel Time is the time in seconds it takes to go at the selected speed from the first signal to this signal.

10. Distance in Cycles (DstCyc)

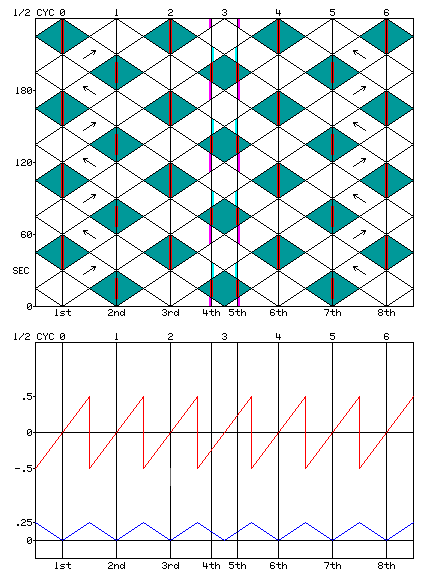
    Distance in Cycles is the time in cycle lengths it takes to go from the first signal to this signal.

11. Distance in Half Cycles (DstHlfCyc)

    Distance in Half Cycles is the time in half cycle lengths it takes to go from the first signal to this signal.

12. Offset Half Cycles (OSHlfCyc)

    Offset Half Cycles is the time in half cycle lengths it takes to go from the master offset point to this signal.

13. Closest Half Cycle (ClosHlfCyc)

    Closest Half Cycle finds the half cycle that is closest to the signal location in time.

14. Half Cycle Error (HlfCycErr)

    Half Cycle Error is the difference between the actual signal position in time and the nearest half cycle, in half cycles.

15. Half Cycle Nearness (HlfCycNear)

    Half Cycle Nearness is the value used to calculate the best phasing for the intersection. Its values range between 0 and 0.25:

    • If HlfCycNear is less than 1/9, a single phase for the progressed road is indicated. This is the best case.
    • If HlfCycNear is between 1/9 and 2/9, a lead-lag left turn phasing is indicated. This is where double alternate progression works best.
    • If HlfCycNear is greater than 2/9, split phase or two greens per cycle is indicated. This is the worst case.

    These limits were chosen to make the software easier to write. But they cover the value range quite well.

16. Bandwidth (Bandwid)

    This is the portion of a cycle useful to progressed cars. Note that a negative value becomes zero.

17. Entire Bandwidth (EntBandwid)

    This is the smallest of the bandwidth calculations. It gives the overall bandwidth available as a fraction of the cycle length.

THE TIME-SPACE DIAGRAM

The time-space diagram is the tool traditionally used to figure progression before computers were commonly used in traffic engineering.

How it works.

• Upper Diagram - The Time-Space Diagram:
  • The horizontal axis shows the distance between signals, adjusted for speed.
  • The vertical axis shows the passage of time, with time flowing upward.
  • The diagonal lines are at the slope of the calculated line.
  • The white bands are the green times.
  • The dark blue-green areas are the spaces between the platoons.
  • The red bars are red lights at the intersections.
  • The cyan bars are places where a leading left turn stopping traffic on the colored side is appropriate.
  • The magenta bars are places where a lagging left turn stopping traffic on the colored side is appropriate.
• Lower Diagram - The Method Used in the Program:
  • The red trace is Half Cycle Error (HlfCycErr), measured in half cycles.
  • The blue trace is Half Cycle Nearness (HlfCycNear)

    Half Cycle Nearness is the value used to calculate the best phasing for the intersection. Its values range between 0 and 0.25, measured in half cycles. The following table shows the best phasings:

Links:

• Signal Progression
• Signal Progression Calculator
• Unusual Traffic Problems and Solutions