Plurality Voting Pie Chart
AN EXAMPLE OF PLURALITY VOTING ERROR:
The example setting:
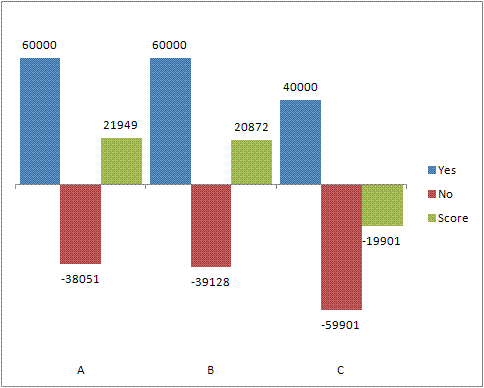
- This is in a town of 100,000 people.
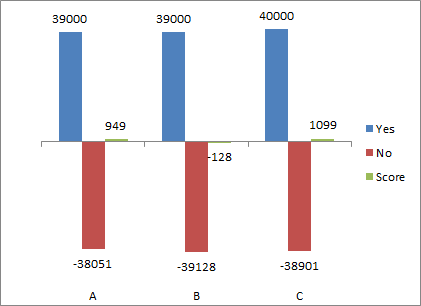
- 40,000 of them support a new zoning ordinance. 60,000 oppose it.
- Three candidates are running for mayor: A, B, and C.
- Candidate C supports the new zoning ordinance. A and B do not.
The election (using the Plurality Voting System):
- Because candidates A and B are similar candidates, voters had to choose which to vote for.
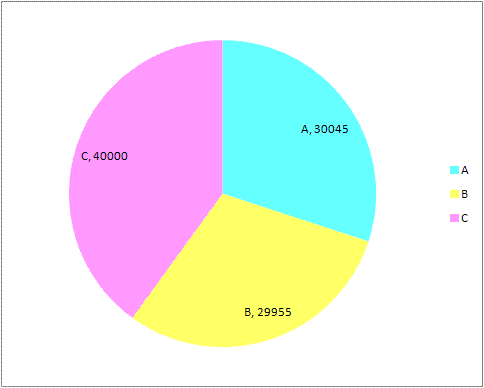
- The election results: A: 30045, B: 29955, C: 40000.
- C wins the election and becomes mayor.
- The mayor implements the new zoning ordinance.
- The will of the public is thwarted. 60 percent of them are unhappy.
The outcome does not match public opinion.
A pie chart in the face!