TUNGSTEN BULB PROPERTIES
THE NON-OHMIC BEHAVIOR OF FILAMENTS
Those who use circuitry containing incandescent filament lamps may have noticed that often the
circuits do not behave the way they expect them to. The current in the circuit does not equal the
current calculated using Ohm's law. This article explores the properties of non-ohmic materials
such as tungsten.
OHM'S LAW
| Variable symbol | Unit of measure | Description |
|---|
| E or V | V = Volts | The force to move electrons |
| I or A | A = Amperes (amps) | The movement of electrons |
| R | Ω = Ohms | Resistance to the flow of electrons |
| P or W | W = Watts | Power - capacity to do work |
| t | K = Kelvin | Absolute temperature (SI) |
| ρ | Ω m = Ohm meter | Resistivity |
| τ | Δ/K | Resistive temperature coefficient |
| | Kelvins | Celsius |
Rankines | Fahrenheit |
| Condition | K | °C |
R | °F |
| Absolute Zero | 0 K | -273°C |
0 R | -460°F |
| Water freezes | 273 K | 0°C |
460 R | 32°F |
| Room Temperature | 298 K | 25°C |
537 R | 77°F |
| Water boils | 373 K | 100°C |
640 R | 212°F |
The electrical equations of Ohm's law and non-ohmic calculations use these basic units of
measure:
Ohm's law consists of these two basic equations:
These two equations can be algebraically combined to find any of the values from any two of
the other values.
- P = I^2 * R
- P = E*2 / R
- R = E*2 / P
- R = P / I^2
Absolute Zero is the coldest that anything can get.
The Kelvin scale starts at absolute zero and uses the Celsius degree.
The Rankine scale starts at absolute zero and uses the Fahrenheit degree.
Resistivity is the measure of the resistance of a material as a 1 meter cube with full face
electrodes on opposite faces.
Resistivity ρ = R * l / A
where R is resistance (Ω), l = length (m), and A = area (m^2)
Temperature coefficient is the change in resistance per kelvin degree.
Tungsten (W) resistivity ρ = 5.6 Ωm and Temp Coefficient
α = .0045/°K.
OHMIC vs NON-OHMIC
Ohmic materials always have the same electrical resistance at most temperatures.
Non-ohmic materials change their resistance with temperature.
When trying to calculate resistivity, you need the length and the cross-section of the conductor.
These are not usually found in bulb specifications.
Most non-ohmic metals change resistance linearly. This makes the job easier.
With an ohmic resistance, the current increases linearly as the voltage increases linearly.
With a linear non-ohmic resistance, the power and resistance increase linearly as the voltage
increases linearly.
Since the tungsten resistance increases linearly with voltage, calculation for tungsten
filament light bulbs is easier. You do not have to figure resistivity.
You will need the following tools for these experiments:
- A multimeter (volts/ohms/milliamps)
- An AC Ammeter
- A wattmeter
- A spreadsheet
- The parts to make the circuits.
- The light bulbs needed
FINDING VALUES FOR A NON-OHMIC TUNGSTEN LIGHT BULB
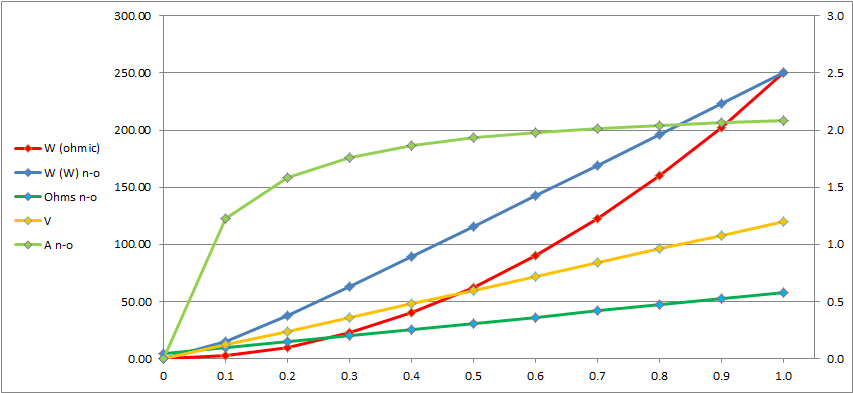
| PART | | 0.0 | 0.1 |
0.2 | 0.3 | 0.4 |
0.5 | 0.6 | 0.7 |
0.8 | 0.9 | 1.0 | |
| V | ↑ | 0 | 12 |
24 | 36 | 48 | 60 | 72 | 84 |
96 | 108 | 120 | |
| V^2 | | 0 | 144 |
576 | 1296 | 2304 | 3600 | 5184 | 7056 |
9216 | 11664 | 14400 | |
| W ohmic | ↑ | 0.0 | 2.5 |
10.0 | 22.5 | 40.0 | 62.5 | 90.0 | 122.5 |
160.0 | 202.5 | 250.0 | |
| W (W) n-o | ↑ | 0.00 | 14.68 |
38.10 | 63.44 | 89.51 | 115.94 | 142.57 | 169.33 |
196.17 | 223.06 | 250.00 | |
| Ω n-o | ↑ | 4.50 | 9.81 |
15.12 | 20.43 | 25.74 | 31.05 | 36.36 | 41.67 |
46.98 | 52.29 | 57.60 | |
| A n-o | | 0.000 | 1.223 |
1.587 | 1.762 | 1.865 | 1.932 | 1.980 | 2.016 |
2.043 | 2.065 | 2.083 | ↑ |
In this experiment, a 250 W 120 V heatlamp is used.
Use the lamp values in the experiment
Find the cold resistance. Measure the lamp filament with the ohmmeter.
I measured 4.5 Ω.
Calculate the lit resistance. Square the 120 V and divide by the 250 W.
This makes 57.6 Ω.
Divide the lit resistance by the cold resistance to find the resistance ratio.
In this case, the ratio is 12.8.
Subtract the cold resistance from the lit resistance to find the span.
In this case, the span is 53.1.
Make a scale in a row on the spreadsheet from 0 to 1 in steps of 0.1.
Make a row of voltages which are 120 V times the scale numbers.
Make a row which is the square of each voltage in the voltage row.
Find ohmic power:
Divide each squared voltage by lit resistance (57.6 Ω here).
Find non-ohmic resistance:
Multiply the span by each scale number, then add cold resistance.
Find non-ohmic power:
Divide each squared voltage by its non-ohmic resistance.
Find non-ohmic current:
Divide each voltage by its non-ohmic resistance.
PROPERTIES
If the bulb is not available to be measured, one tenth of the calculated lit resistance works as an estimate
for the cold resistance.
The ohmic resistance is flat, and the ohmic voltage and current are linear. The ohmic power is a second-power
function.
The non-ohmic resistance, voltage, and power are linear. The current is a diminishing rising curve.
CONNECTING IDENTICAL NON-OHMIC TUNGSTEN LIGHT BULBS IN SERIES
We used to just use ohm's law to figure lamps in series. But now we know that this is wrong.
USE THIS PROCEDURE TO MAKE THIS TABLE:
| Lamps (L) | 1 |
2 | 3 | 4 |
5 |
| 1/L | 1.00 |
.50 | .33 | .25 | .20 |
| V/L | 120 |
60 | 40 | 30 | 24 |
| V^2 | 14400 |
3600 | 1600 | 900 | 576 |
| W/L ohmic | 250 |
62.5 | 27.8 | 15.6 | 10 |
| Wt ohmic | 250 |
125 | 83.3 | 62.5 | 50.0 |
| At ohmic | 2.083 |
1.042 | 0.694 | 0.521 | 0.417 |
| W/L (W) n-o | 250.0 |
115.9 | 72.1 | 50.6 | 38.1 |
| Wt (W) n-o | 250 |
231.9 | 216.2 | 202.5 | 190.5 |
| Ω/L n-o | 57.6 |
31.1 | 22.2 | 17.8 | 15.1 |
| At n-o | 2.083 |
1.932 | 1.802 | 1.688 | 1.587 |
CALCULATE YOUR OWN SERIES:
This is a series of 4 identical lamps.
Use the lit 120 V and lit 250 W from the package.
Calculate 1 bulb lit resistance: 120 ^ 2 / 250 = 57.6 Ω
Measure cold resistance of 1 bulb. I got 4.5 Ω
Subtract cold resistance from lit resistance to get span 53.1 Ω
Divide span by 4 lamps to get individual lamp span 13.3 Ω
Add result to cold resistance for series lamp resistance 17.8 Ω
Multiply lamp resistance by 4 to get total resistance 71.2 Ω
Divide 120 V by total lamp resistance to get total current 1.69 A
Multiply 120 V by 1.69 A to get total power 202 W
Divide total power by 4 to get each lamp power 50.5 W
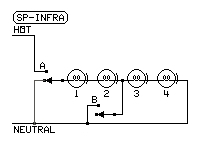
The page author uses this circuit to add infrared warmth to a room without blasting it in heat.
Switch B adds heat by leaving two bulbs out of the series.
In this experiment, several 250 W 120 V heatlamps are used. Use the lamp values in the experiment
Find the cold resistance. Measure the lamp filament with the ohmmeter. I measured 4.5 Ω.
Calculate the lit resistance. Square the 120 V and divide by the 250 W. This makes 57.6 Ω.
Subtract the cold resistance from the lit resistance to find the span. In this case, the span is 53.1.
Make a scale in a row L (number of lamps) on the spreadsheet from 1 to 5.
Make a row of values 1/L.
Make a row of voltages which are 120 V divided by the number of lamps.
Make a row which is the square of each voltage in the voltage row.
Find ohmic power per lamp for each number of lamps:
Divide each squared voltage by lit resistance (57.6 Ω here).
Find total ohmic power for each number of lamps:
Multiply ohmic power per lamp by the number of lamps).
Find ohmic current:
Divide each voltage by lit ohmic resistance (57.6 Ω here).
Find non-ohmic resistance:
Divide the span by the number of lamps, then add cold resistance.
Find non-ohmic power per lamp:
Divide each squared voltage by its non-ohmic resistance.
Find non-ohmic total power:
Multiply each power per lamp by the number of lamps.
Find non-ohmic current:
Divide each lamp voltage by its non-ohmic resistance.
PROPERTIES
The resistance of each of the identical lamps in a series circuit is the same.
The resistances of the lamps depend on the number of lamps in series.
The power in the circuit is larger than using ohm's law with the lit resistance.
It is possible that the actual properties of the bulbs used are different.
If this is the case, the actual properties of a series of identical lamps can be found as follows:
- Use an AC ammeter to measure the actual current in the operating circuit.
- Divide the 120 V by actual current to get the total operating resistance.
- Multiply 120 V by actual current to get total power.
- Divide 120 V by number of lamps to get lamp voltage.
- Divide total operating resistance by number of lamps in series to get lamp operating resistance.
- Divide total power by number of lamps to get lamp power.
CONNECTING DIFFERENT NON-OHMIC TUNGSTEN LIGHT BULBS IN SERIES
It is easier to construct the circuit and take measurements than it is to calculate the values.
I built a box with two duplex outlets wired in series across the 120 V feed to design the circuit. They
should not be used in the finished design.
The safety grounds of the duplex outlets are connected to the source safety ground.
Put the bulbs in portable lamps to test the circuits.
Plug one of the lamps into one socket in each duplex outlet. The other socket in each duplex is for test
prods.
- Switch all of the lamps on.
- Use an AC ammeter to measure the actual current in the operating circuit.
- Use the multimeter in AC V to get lamp voltage across each lightbulb (use second socket in each duplex)
- Divide each lamp voltage by actual current to get each lamp operating resistance.
- Multiply each lamp voltage by actual current to get lamp power for each lamp.
- Divide 120 V by actual current to get total operating resistance. It should be sum of lamp operating
resistances.
- Multiply 120 V by actual current to get total power. It should be the sum of lamp powers.
CONNECTING A NON-OHMIC NICHROME HEATER TO A LOWER VOLTAGE
Experiments have shown that the temperature coefficient of nichrome is so low that Ohm's law does the job.
In the unit I tried, the cold resistance 113 Ω was only 2 Ω lower than the calculated
resistance 115.2 Ω.
In this application, a 240 V 500 W heater is run at 120 V.
Calculate operation at 240 V:
Square the 240 V to get 57600.
Divide 57600 by 500 W to get resistance 115.2 Ω
Divide 500W by 240 V to get current 2.083 A.
Now calculate operation at 120 V:
Divide 120 V by 115.2 Ω to get current 1.042 A
Multiply 120 V by 1.042 A to get power 125 W
PROPERTIES
When the voltage is halved, the current is divided by 2 and the power is divided by 4.
This is useful for making a low-power heater.
SPECIAL USES FOR NON-OHMIC TUNGSTEN LIGHT BULBS
The linear change of resistance with voltage or wattage has some interesting uses:
- LOAD TO KEEP LED CHRISTMAS LIGHTS FROM BURNING OUT
Sometimes a voltage surge can cause LEDs to burn out. Connecting a low-wattage incandescent lamp in
series with the LEDs absorbs the shock of the surge. Connecting two lamps of different wattage can
make a voltage divider to reduce the voltage of DC lamp drivers. Use two lamps in series to get values
you can't buy.
- LOAD TO PREVENT FAILURE OF TRANSISTORS IN AN AUDIO POWER AMPLIFIER
Sudden transients in the signal can shock an output transistor in an audio amplifier into semiconductor
avalanche breakdown. This can destroy the transistor. The bulb provides a variable resistance load to
prevent the avalanche.
- LOAD TO SOFTEN THE CHARGING OF A POWER SUPPLY CAPACITOR
In my job, we were building a high-voltage capacitor-discharge supply to pulse a solenoid to provide
a sudden motion for a scientific experiment. The problem was that the capacitor often blew when recharging.
But a series resistance in the charging circuit made it charge too slowly for the next pulse. A light bulb
as the current limiter worked.
- AUTOVARY SEPARATION ENHANCEMENT FOR SURROUND SOUND DECODER
In matrix surround sound, the separation between channels is low. One of the big problems is the center
soloist appears in the back channels. This Autovary circuit (light bulb in circuit at right) changes the
decoding angle of the back channels when a front soloist is predominant to reduce the signal from the front
soloist in the back speakers.
Many separation-enhancement systems for surround sound have the problem with "pumping". This is a problem
where the actions of the separation enhancement are audible as sudden changes in level for some parts or
noise levels. Due to the linear behavior of tungsten's temperature coefficient and the timing of the change
in resistance, the Autovary system shows no side-effects of the separation enhancement.
STANDARD METHOD FOR TUNGSTEN LIGHT BULBS
| V ratio |
R redux 10 |
P redux 10 |
. |
R redux 8 |
P redux 8 |
| 1.00 | 1.000 | 1.0000 | . | 1.0000 | 1.0000 |
| 0.90 | 0.910 | 0.8901 | . | 0.9125 | 0.8877 |
| 0.80 | 0.820 | 0.7805 | . | 0.8250 | 0.7758 |
| 0.75 | 0.775 | 0.7258 | . | 0.7813 | 0.7200 |
| 0.70 | 0.730 | 0.6712 | . | 0.7373 | 0.6644 |
| 0.67 | 0.703 | 0.6385 | . | 0.7113 | 0.6311 |
| 0.60 | 0.640 | 0.5625 | . | 0.6500 | 0.5538 |
| 0.50 | 0.550 | 0.4545 | . | 0.5625 | 0.4444 |
| 0.40 | 0.460 | 0.3478 | . | 0.4750 | 0.3368 |
| 0.33 | 0.397 | 0.2743 | . | 0.4138 | 0.2632 |
| 0.30 | 0.370 | 0.2432 | . | 0.3875 | 0.2323 |
| 0.25 | 0.325 | 0.1923 | . | 0.3438 | 0.1818 |
| 0.20 | 0.280 | 0.1429 | . | 0.3000 | 0.1333 |
| 0.10 | 0.190 | 0.0526 | . | 0.2125 | 0.0471 |
| 0.00 | 0.100 | 0.0000 | . | 0.1250 | 0.0000 |
Procedure for using the formulas:
- Calculate the Hot resistance of the bulb at full voltage:
Square the rated voltage, then divide by the rated wattage.
- Choose which of these to use to get the Cold resistance of the bulb:
- Use the guesstimate of 1/10 of the hot resistance.
- Use an ohmmeter to measure the Cold resistance of the lamp.
- Calculate resistance Span, ColdPortion, SpanPortion, and voltage reduction Ratio:
- Span = Hot − Cold
- ColdPortion = Cold / Hot
- SpanPortion = Span / Hot
- Ratio = OperatingVoltage / rated voltage
- Calculate the R_redux (reduced resistance at operating voltage):
R_redux = Cold + Span * Ratio
- Calculate the P_redux (reduced power at operating voltage):
P_redux = OperatingVoltage ^ 2 / R_redux
It's too bad the government wants to get rid of filament light bulbs. They have uses beyond illumination.