ANIMATED TRIGONOMETRY CONSTRUCTION

See How Trigonometry Works

Trigonometry is often easier to understand if you can see it in action. Here are some constructions and animations to show how it works:

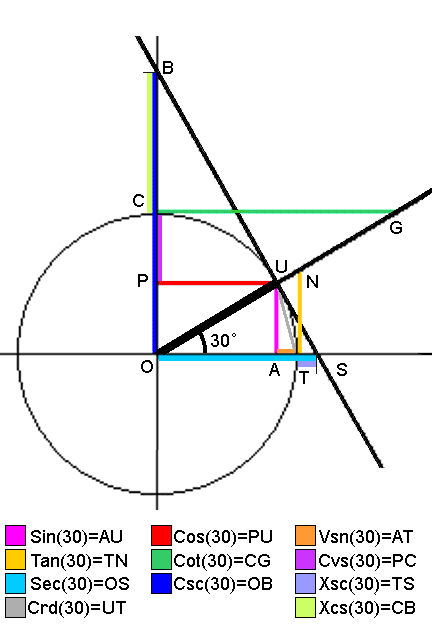
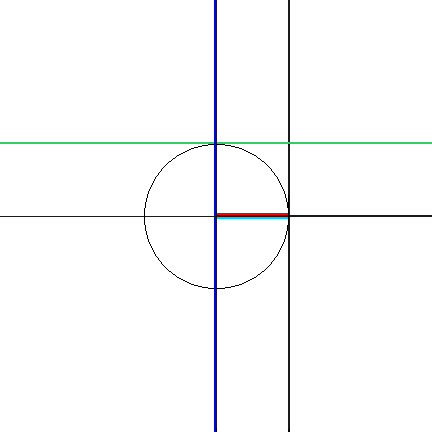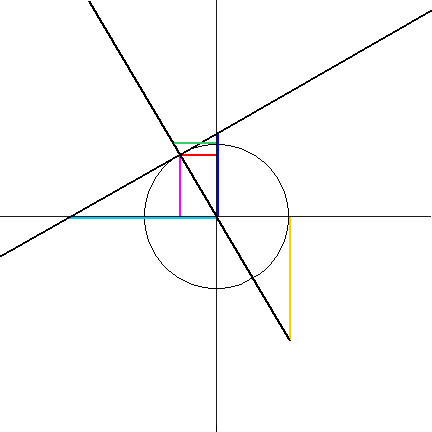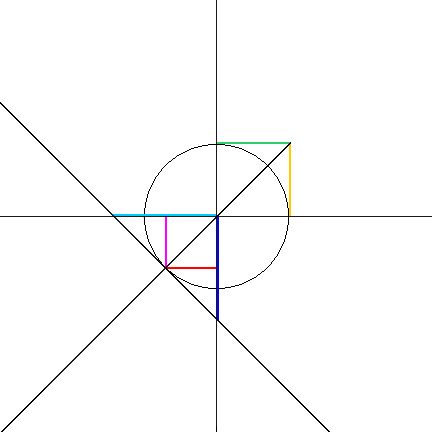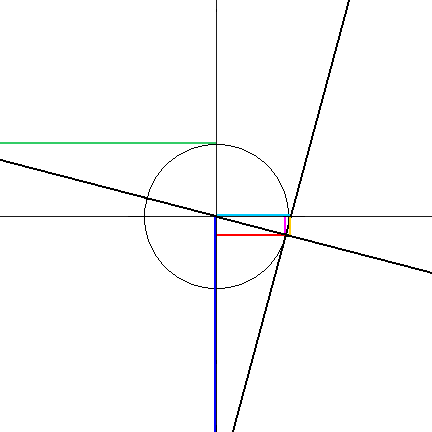
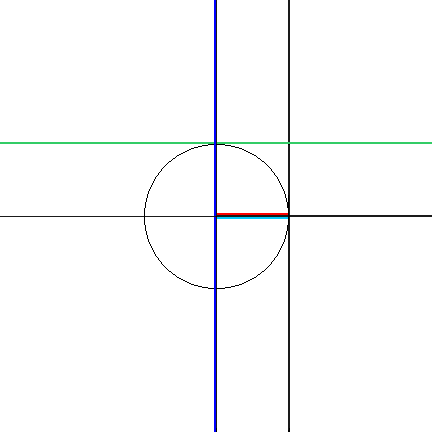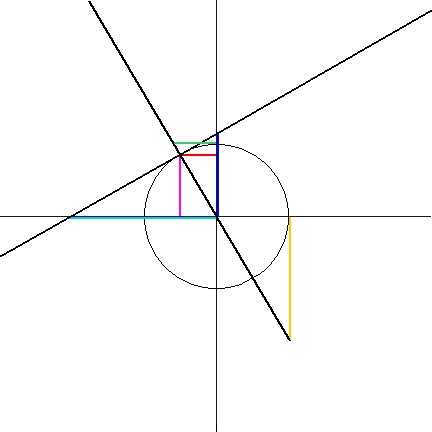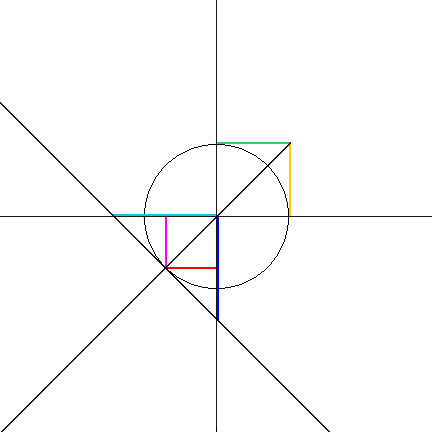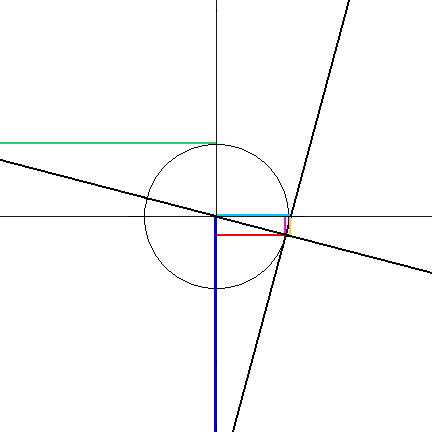
Constructing the trigonometric functions from the unit circle:

  1. Construct a unit circle centered on the origin (0, 0).
  2. Place the angle TOU in standard position, with leg OT on the positive x axis and the vertex O at the origin.
  3. Extend the ray OU that defines the angle beyond the unit circle.
    If it is not in the first (upper right) quadrant, extend an "opposite ray" in the opposite direction from O.
  4. Construct line SB tangent to the unit circle at U and perpendicular to ray OU.
    Point S is always on the x axis, and point B is always on the y axis.
  5. Construct segments AU, PU, TN, and CG. All are perpendicular to the axis they intersect.
  6. Note that point T is always at (1, 0), no matter which quadrant ray OU is in.
    If ray OU is in a left side quadrant, construct TN to the opposite ray instead.
  7. Note that point C is always at (0, 1), no matter which quadrant ray OU is in.
    If ray OU is in a lower quadrant, construct CG to the opposite ray instead.

Note that, since there are three sets of congruent triangles, the values can be obtained at more than one location. But the constructions given here always provide the correct sign for each function.

Reading trigonometric values from the constructions:

  • The sine (sin) of the angle is segment AU. It is positive if U is above A, and negative if U is below A.
  • The cosine (cos) of the angle is segment PU. It is positive if U is to the right of P, and negative if U is to the left of P.
  • The tangent (tan) of the angle is segment TN. It is positive if N is above T, and negative if N is below T.
    The tangent is the slope of ray OU.
  • The cotangent (cot) of the angle is segment CG. It is positive if G is to the right of C, and negative if G is left of C.
  • The secant (sec) of the angle is segment OS. It is positive if S is right of O, and negative if S is left of O.
  • The cosecant (csc) of the angle is segment OB, It is positive if B is above O, and negative if B is below O.

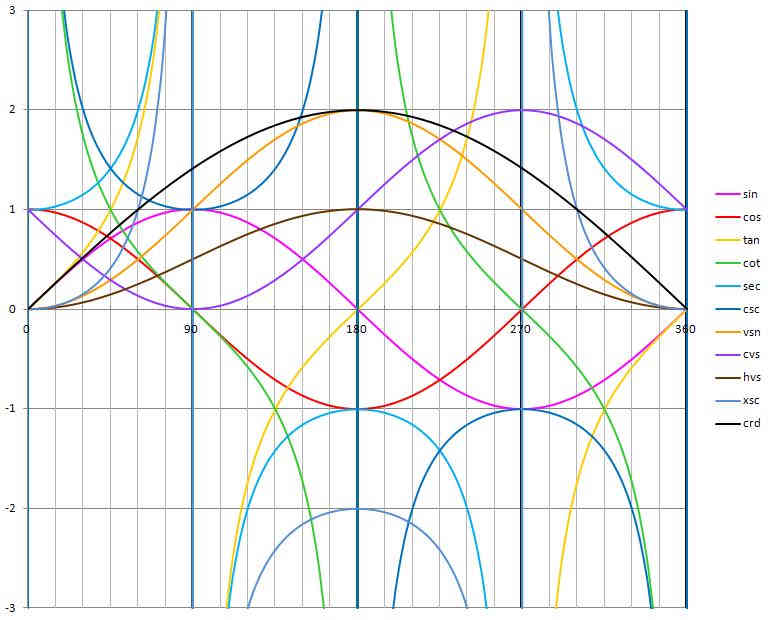
Other Trigonometric Functions:

These trigonometric functions were used in global navigation before the inventions of logarithms and the Harrison marine chronometer.

  • The chord (crd) is twice the sine of half the angle.
    crd(θ) = 2 sin(θ/2)
  • The versine (vsn) of the angle is the "verted sine." It is segment AT, and is always positive.
    vsn(θ) = 1 - cos(θ)
  • The coversine (cvs) of the angle is the verted cosine. It is segment PC, and is always positive.
    cvs(θ) = 1 - sin(θ)
  • The haversine (hvs) of the angle is half of the versine. It is half the length of segment AT, and is always positive. It is useful in great circle navigation calculations.
    hvs(θ) = vsn(θ)/2
  • The exsecant (xsc) of the angle is the exterior secant. It is segment TS, and changes sign. It is the part of the secant outside the circle.
    xsc(θ) = sec(θ) - 1
  • The excosecant (xcs) of the angle is the exterior cosecant. It is segment CB, and changes sign. It is the part of the cosecant outside the circle.
    xcs(θ) = csc(θ) - 1

The congruent triangles in the construction:

CONGRUENT
TRIANGLES		FORMULA ILLUSTRATED
OAU & UPOsin(θ)2 + cos(θ)2 = 1
OTN & OUStan(θ)2 + 1 = sec(θ)2
OCG & OUBcot(θ)2 + 1 = csc(θ)2

All of these triangles are similar, and all of them contain an angle congruent to angle TOU.

Trig constructions

The Trigonometric Functions in Action:

Watch the sizes of the constructed trigonometric functions change as the angle changes.
The colors are the same as in the construction diagram above.

Trig animations

Here it is in slow motion, so you can see the changes:

Trig slow animations

Here is a graph of the trigonometric functions over a range of 360 degrees or 2π radians:

Trig chart

Science and Measurement